Математика коронавируса

В связи с пандемией COVID-19 по сети бродит масса довольно наивных концепций о моделировании эпидемий. Попробуем разобраться. Мы только рассмотрим математические методы моделирования заразных болезней, касаясь медицины и биологии лишь когда требуется прикинуть какой-нибудь параметр.

Экспонента или сигмоида?

Наш первый учебно-тренировочный (там в стволе дырочка, если что) вирус будет простой. В начальный момент времени (нулевой день), t=0, полагаем что есть один инфицированный (то есть заражённый), скажем, некая старушка на рынке в Ухане, заразившаяся мутировавшим вирусом. Вирус новый, ни у кого в популяции нет к нему иммунитета. Время t будем измерять в сутках, считая нулевым день, когда мутировавший вирус заразил нашу гипотетическую бабушку. Также пока предположим, что наш вирус вообще не вызывает никаких симптомов, и поэтому ни лечения, ни изоляции инфицированных не проводится, так как заболевших и умерших нет. С точки зрения биологии, это «идеальный вирус» – он продолжает свой геном, не уменьшая количества носителей (людей). Мы также полагаем, что однажды инфицированный быстро освободиться от вируса не может, по крайней мере десяток лет. Это примерно как вирус герпеса – он на всю жизнь, но его почти не заметно. Инкубационный период нашего вируса пусть измеряется минутами. Как в Голливудском ужастике про эпидемию. Но у нас вирус с дырочкой в стволе, нам не страшно.

Простейшее рассуждение – распространение вируса по экспоненте. Классическая математика из программы средней школы: геометрическая прогрессия, задачка о рисе на шахматной доске, и тому подобное. Пусть каждый инфицированный каждый день заражает, например, r_exp=2 человек. В нулевой день, один инфицированный: бабушка с рынка. В первый день, три инфицированных: бабушка, внук и внучка (внук плюс внучка – это 2, то есть r_exp). Помним, что смертей и вообще симптомов наш вирус не вызывает, оттого ни бабушка, ни внуки, ни окружающие не знают, что у них вирус. Во второй день, девять инфицированных: бабушка, её внуки, родители внуков, четыре одноклассника внуков в школе. Ну и так далее. На 21-й день число заражённых превысит всё население Земли: (r_exp+1)²¹ = 3²¹ = 10.5 млрд.

Ясно, что геометрическая прогрессия неплохо работает в начальном периоде распространения вируса, но затем начинает выдавать сильно завышенные результаты. Мы попробуем решить задачку не в лоб, а правильно. Как её решают в университетах, а не в школах.

Пусть P=Const – вся популяция (рождаемость и смертность в модели рассматривать не будем). I(t) человек – количество инфицированных новым вирусом;. Трансмиссивность (это «передаваемость», не путать с «контагиозностью»-заразностью и «вирулентностью»-способностью вызывать болезнь) r=Const измеряется в ⅟сутки – это показатель, какое число здоровых людей может быть инфицировано в среднем одним инфицированным за день. В качестве численного примера положим, что r=1, P = 7.8 10⁹ (последнее значение примерно как население Земли в 2020 году). Слова «в среднем» и «за день» у нас тут выделены. Мы к ним вернёмся. Забегая вперёд также заметим, что r выше – это не та R₀, о которой шумит весь Интернет. До R₀ мы тоже доберёмся позже.

Прирост числа инфицированных I (infected) от времени записывается обыкновенным дифференциальным уравнением:

Это классическое уравнение Мальтуса-Ферхюльста, где константа r – эквивалент коэффициента рождаемости b, а P – это равновесная популяция P₀ из оригинальной формулы Мальтуса. Уравнение решается аналитически. Как выводится, пояснять не будем для краткости, тут не важно. Решение уравнения {1} – это сигмиода, она же «логистическая функция» (Sig), а её первая производная – функция Хабберта (Hubb):

Достаточно проверить решение прямой подстановкой выражений {2}, {3} в уравнение {1}.

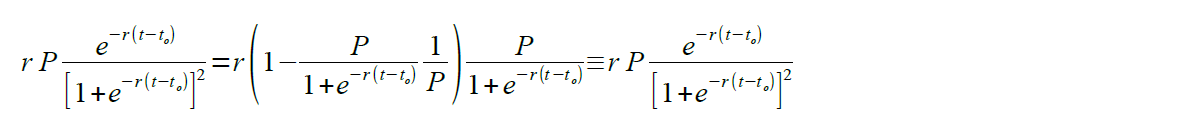
Тождество левой и правой частей очевидно при любом t₀. Точка t₀ – это точка максимума функции Хабберта, её мы будем подбирать из граничных условий. Мы знаем, что в нулевой день t=0 инфицирована только старушка с рынка. Значит,

Максимум заразившихся будет на 23-й день. По формуле {3}, в эти критические сутки заразится:

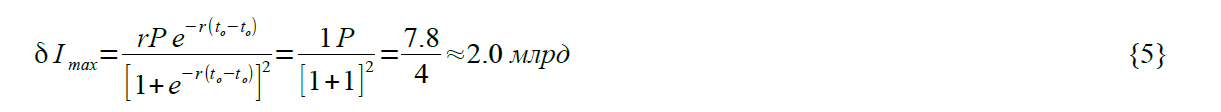
Последний не заразившийся (вообразим такого охотника-одиночку из племени Умба-Юмба) будет на 2t₀, то есть в нашем случае примерно на 46-й день распространения вируса по планете. Доказываем аналитически:

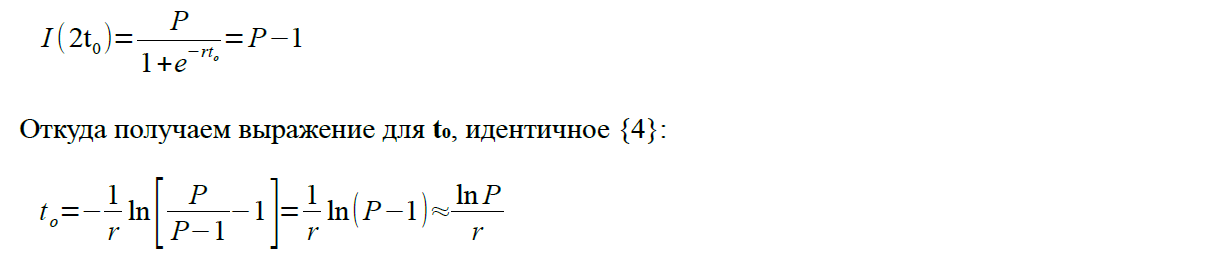
Каждый может проверить, что функция Хабберта – симметрична относительно точки t₀. Теперь нарисуем два графика: нашу сигмоиду и экспоненту. Легко обнаружить, что первые несколько дней экспонента и сигмоида близки. Если I много меньше P, то:

Экспонента у нас была с параметром r_exp = 2, для сравнения положим r = ln(2+1) ≈ 1.1. Тогда t₀ = ln(7.8·10⁹)/1.1 ≈ 20.7.

Вплоть до 10-го дня распространения вируса (отсчёт с нуля, а не с единицы), сигмоида и экспонента идут нос-к-носу. На 11-й день, по экспоненте получается 3¹¹=177'147, a по сигмоиде 177'143. Далее экспонента безудержно и навсегда обгоняет сигмоиду. На 18-й день разница уже примерно 18 миллионов, или 5%. В последний, 42-й день, распространения вируса, 7.8 миллиарда заразных гоняют по всей планете одного-единственного незаразного (того охотника-одиночку из Умба-Юмба). Экспонента в этот день где-то в космосе: 10²º человек.

Надо сделать оговорку, что в начале – первые сколько-то дней – обе модели не верны. Бабушка с рынка наверняка заразит в первый день не только двух внучат, а ещё, к примеру, пятерых покупателей. Заразная бабушка одна, но здоровых покупателей вокруг много, вирусу есть где разгуляться. Далее эти покупатели понесут вирус другим продавцам, то есть в это время r_exp > 2. И наоборот, если бы вирус подхватил охотник-одиночка в джунглях, он таскал бы его с собой много дней, не заражая никого r = r_exp = 0, пока не пришёл бы в деревню. И экспонента, и сигмоида начинают нормально описывать распространение заразы, только когда число заразных переваливает примерно за сотню или тысячу (два-три порядка), и начинается «статистика», а не «стохастика».

В конце периода распространения вируса экспонента не работает по определению; там миллиарды триллионов не существующих заражённых. Сигмоида может работает примерно до момента, когда осталось несколько тысяч незаразных. Всех до последнего человека вам не заразить, даже если очень стараться. Полковник Пупкин! Оставайтесь в бункере!

Вообще мы не знаем вирусов, способных заразить всё население планеты за месяц-два.

Во-первых, если такие и были, то проявить свою сущность могли лишь примерно с середины XX века, когда стал общедоступным авиатранспорт. До этого, к племени Умба-Юмба надо плыть месяц на пароходе, потом ехать на слонах по джунглям две-три недели. Приехали заражать последнего, а племя говорит: наш одинокий охотник ушёл! То ли на север, то ли вверх по Замбези...

Во-вторых, если такой вирус и существует, то мы про него не узнали! Просто не заметили. Он же скрытный, бессимптомный, никому не мешает. Размножается себе втихаря. Опять-таки, тому примером вирус герпеса, хотя его распространение явно занимает не месяцы, а годы, да и заражены далеко не все, да и кое-какие неприятные симптомы бывают («простуда на губе»… ну или «там»), но об этом чуть ниже.

Полагая, что вирус скрытный, и человек против него никаких мер не принимает, прикинем, очень грубо, реалистические значения r для случая, если заражённые всю жизнь заразны. Пусть вирус втихаря захватывает планету за два года, то есть t₀=365. Из формулы {4}: r = ln(7.8·10⁹) / 365 = 0.06. Если распространение вируса началось, скажем, 1 января, то первый миллион заражённых будет во второй половине августа, а первый миллиард (заметим ещё раз, они не знают, что заражены, симптомов нет) – в конце сентября того же года. Последний миллион не заражённых останется в июле следующего года.

Конечно, с реальными вирусами всё происходит куда медленнее. Не пугайтесь! Сейчас попробуем сделать наш учебно-тренировочный вирус чуть более реалистическим. Дырочку в стволе оставим.

Базовое репродукционное число.

Прежде чем заражённый сам станет заразным, проходит какое-то время. Это инкубационный, он же латентный период. Далее вируса накапливается достаточно, и пациент начинает его «выделять» (или «сбрасывать», shed). Некоторые заболевания, например оспа или полиомиелит, проходят полностью, делая переболевшего незаразным. В других случаях, как у ВИЧ или при гепатите C, заразившийся остаётся потенциально заразным всю жизнь. Мы рассмотрим подробнее первый случай, так как вызывающий болезнь COVID-19 коронавирус, насколько мы знаем, с пациентом не остаётся [1].

По данным ВОЗ [1], инкубационный период COVID-19 – от 1 до 14 дней, в среднем 5-6. У нашего учебно-тренировочного вируса сделаем такой же. Примерно три недели после инфицирования человек становится не заразен.

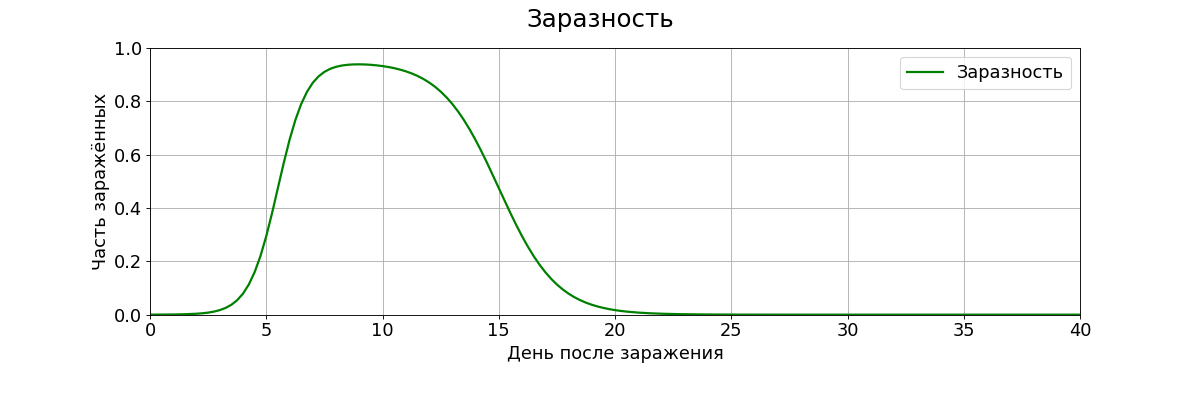
Кривая работает так. Если, скажем, 31 декабря 1000 человек заразилось вирусом, то 1 января заразных среди них нет. К 5 января примерно 300 будут заразными, а 700 – пока нет. Восьмого января примерно 900 заразных. На 21 день заразных среди этой тысячи будет около 20. На 30-й день заразных нет.

Конечно, раз на раз не приходится. У всех возбудителей свои кривые. Кривая выше – просто одна из бесконечного множества вариантов. Числовой пример. Я искал, но не нашёл реальных данных по COVID-19; статьи пока не опубликованы. По всем параметрам моя кривая удовлетворяет отчёту ВОЗ [1], но там только опорные циферки, без картинок.

В сети народ ломает копья, может ли человек заражаться повторно одним и тем же вирусом. По опыту вирусa SARS [5], антитела к коронавирусам вроде бы могут сохраняться у человека до 12 лет после заболевания – с момента эпидемии SARS уже достаточно времени прошло, но конкретно про COVID-19 мы, натурально, не знаем. Те коронавирусы, что вызывают «обычную простуду», иммунитета не оставляют, но в конце концов в отчёте ВОЗ [1] упоминаний повторных заражений у более чем 40'000 лабораторно-подтверждённых случаев за 2 месяца нет. Для нашего учебного вируса положим, что иммунитет на всю жизнь, как от оспы.

Зелёную кривую выше обозначим 0≤ρ(t)≤1 – произвольная неотрицательная функция, ρ(t≤0)=0. Определим число R₀ – вот оно, добрались! Это базовое репродукционное число (basic reproduction number). По-английски произносится «Ар-нот» («нот» как «knot» аки «узел»).

Это площадь подграфика нашей зелёненькой функции заразности, умноженная на трансмиссивность r. Единица измерения – «люди». Столько людей инфицированный может заразить в среднем за период заразности (уже не «в день»), если (а) никаких мер защиты не применять, и (б) вокруг находится достаточно кандидатов для заражения. Верхний предел интеграла t_l – среднее время жизни вирусоносителя с момента заражения. У безобидного вируса из нашего предшествующего примера величина R₀ огромна! Человек заразен с момента инфицирования и до конца жизни, умирает от старости, а не от вируса, сам про заражение не знает. Пусть средняя ожидаемая продолжительность жизни – 70 лет, или около 25'600 дней, r=0.06 – как выше. Тогда r₀=0.06·25'600/2≈770. Средний инфицированный может заразить многие сотни, хотя и не успеет. За период распространения вируса 2t₀ = 730 дней, получится в среднем 44 человека, а далее кандидаты на заражение все кончатся. Ключевое слово, опять-таки, «в среднем». Наша гипотетическая бабушка с рынка никуда не ездит, сидит торгует. В первый день, заразила примерно семерых, во второй день примерно семерых… На, скажем, 15-й день – внезапно ноль! На рынке уже у всех поголовно вирус (они про него не знают, симптомов нет), и по второму разу их тем же вирусом не заразить. Итого примерно 15 дней на примерно 7 человек – то есть около сотни. Последний землянин без вируса, охотник из Умба-Юмба (которого остальные миллиарды заразили на 730-й день) мог бы заразить семьсот с лишним, но заразит ровно ноль. Он же последний!

Для сравнения прикинем, очень грубо, значение для ВИЧ/СПИД. Пусть в среднем человек заражается ВИЧ в возрасте 20 лет и доживает до 55 (всё примерно, для порядка величин). Это 12'800 дней. Пусть вирусоноситель ведёт беспутный образ жизни, с беспорядочными партнёрами, без защиты. Пусть делает «это» каждый день, то есть (а) не применяет мер защиты и (б) имеет множество кандидатов/кандидаток для заражения. Вероятность заразиться при незащищённом сексе примем грубо 1% за (весело проведённые) сутки. Тогда R₀ = 0.01·12'800≈130. Может заразить более сотни! Почему же мы сейчас, через много лет после начала мировой эпидемии, все поголовно не заражены ВИЧ? Ну, «может» не значит «хочет» заражать. Маньяки встречаются, и некоторые заражали до сотни партнёров; были коловшие деткам прививки с одной иглы медсёстры, и так далее, но большинство людей, в том числе инфицированных, всё-таки относятся к заболеванию ответственно. А те, у кого вируса нет, тоже ведь не все дураки. Настаивают на защищённом сексе, требуют справок, избегают случайных связей, не колются одним шприцем, и так далее. «Могут» заразиться – совсем не значит «хотят»!

Тут надо сделать лирическое отступление про остракизм. «Диванные эпидемиологи» без дипломов призывают больных и переболевших чуть ли не сжигать живьём. Ну, если не бомбардировка зажигательными бомбами, как в «Outbreak», то по крайней мере запереть в лепрозорий – на год-другой, либо на всю жизнь. Двадцатого февраля в Новых Санжарах (Украина) автобусы с эвакуированными из КНР согражданами закидали ручными гранатами камнями. Насколько известно, 5 марта всех несчастных закиданных выписали по домам. Среди них лиц с коронавирусом не оказалось.

Говорят: «Но мы же на всякий случай! Мы же защищаем здоровых!» В конце XX века экстремисты по всему миру точно так предлагали бороться с ВИЧ/СПИД (сначала «они же все гомики», потом «они же все гомики и наркоманы», потом «они же все гомики, наркоманы и негры», и так далее). Квалифицированный врач такого совета ни в жизнь не даст. Это потому, что все врачи, в том или ином виде, дают клятву, которую иногда (технически неверно) называют «клятвой Гиппократа». Так вот. Предложение применять к заболевшим меры, сверх необходимых и достаточных приводит лишь к тому, что заболевшие начинают (буквально) чихать на окружающих. Уважаемые блоггеры! Внимательно читаем «Кулау-прокажённый» Джека Лондона. Чешем репу.

Теперь вернёмся к нашему учебно-тренировочному вирусу. Площадь подграфика посчитаем численно. Получается R₀/r=9.0. Для COVID-19 китайские специалисты насчитали пока R₀=2.3, ВОЗ согласилась. Следовательно, трансмиссивность r должна быть довольно высокой: примерно r = 2.3/9.0 = 0.255. Впрочем, ожидаемо. По отчёту ВОЗ вирус распространяется при кашле и чихании (с мокротой), попадает на предметы, далее мы его тащим немытыми руками на лицо. Ну или чужая мокрота летит вам в лицо (приятного аппетита!). Нет, передача по воздуху«сухих» (без мокроты) вирусных частиц – не подтвердилась.

Уравнение {1} теперь записывается как система:

Здесь C(t) – количество заразных (contagious), S(t) – количество людей, которые могут заразиться вирусом (susceptible).

Формула немного зубодробительная, но смысл такой. Если в нулевой день у вас один заражённый, I(0)=1, то заразных ноль, C(0)=0 – смотрим на кривую заразности выше. То же самое и на второй день. На пятый-шестой день, «нулевой» пациент становится заразен, I(6)=1, C(6)=1, но пока никого не заразил. На седьмой день, заражённых, например, шесть, но заразен по-прежнему лишь «нулевой», I(7)=6, C(7)=1. Так продолжается до 11 дня, когда заразившиеся на 6-й день сами становятся заразны I(11)=31, C(11)=7. На 12-й день становятся заразны заразившиеся в день номер 7: I(12)=67, C(12)=12. Ну и так далее. Решать систему {8} будем численно. Там есть аналитические подходы типа уравнения Мак-Кендрика, но уж очень всё тоскливо. Для сравнения, на том же графике пунктиром показано аналитическое решение для случая, если вирусоносители заразны всю жизнь.

График отвечает на вопрос «что будет с коронавирусом, если правительства ничего не станут делать?» В нашем численном примере такая постановка вопроса законна, потому что наш численный вирус не вызывает не только смертей, но и симптомов, то есть люди про вирус вообще не знают. В реальном мире от COVID-19 можно умереть, поэтому по крайней мере одна страна уже озаботилась. Это КНР, то есть 18% человечества. Поэтому график имеет лишь теоретическую ценность. Так уже не будет.

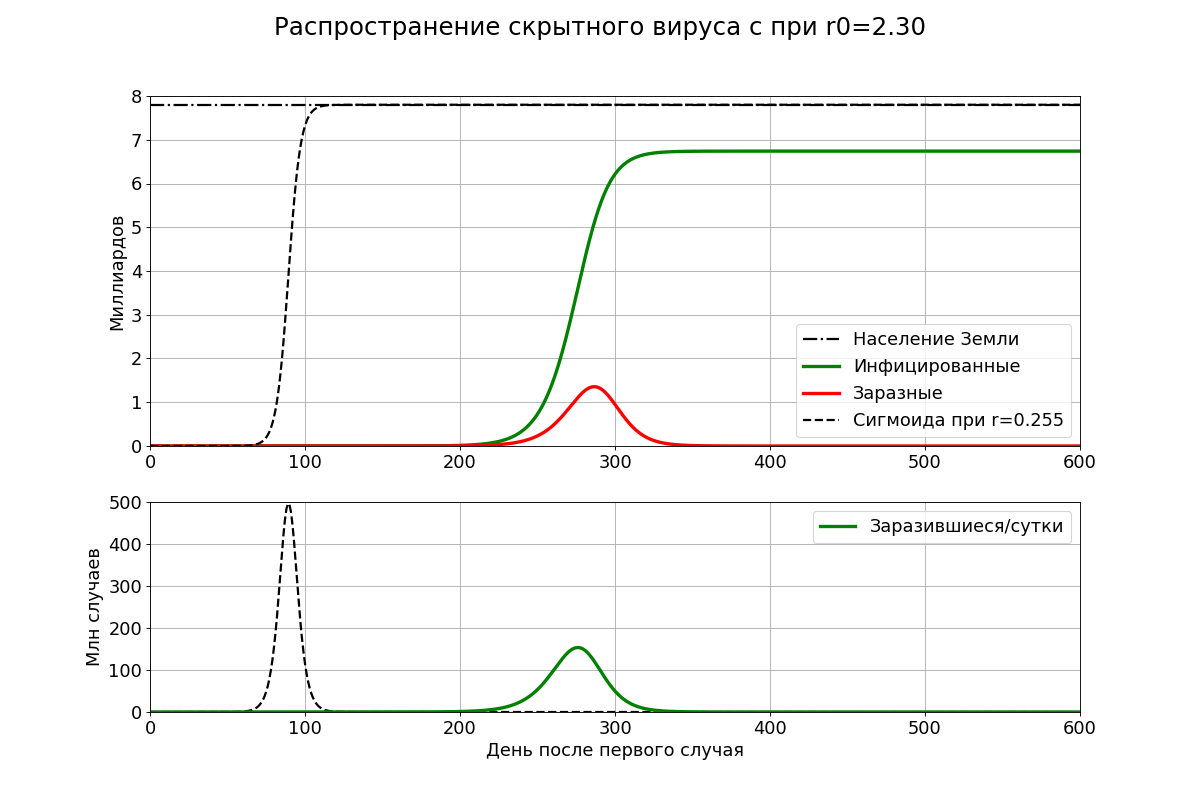
Пик заражений наступает примерно на 280-й день. В этот день заразится 150 млн человек. На 290 -й день будет пик заразных: около 1.3 млрд. Далее распространение вируса замедлится. К 400-му дню на планете останется более миллиарда тех, кого вирус не тронет. Это не потому, что они прятались где-то в тайге – у нас в модели изоляции совсем не предусмотрено. Эти люди гуляли вместе со всеми заразными (никто же вообще не знает, что вирус существует!), но заразиться не успели до того, как вирус полностью «выгорел». Примерно так же в топливных элементах атомных реакторов остаются «не выгоревшие» атомы урана-235, а химических реакциях – не прореагировавшие молекулы исходных реагентов.

Переменное репродукционное число. Дистанцирование.

В Интернете модно выдавать страждущим примерно вот такие советы (писано вроде 13 марта):

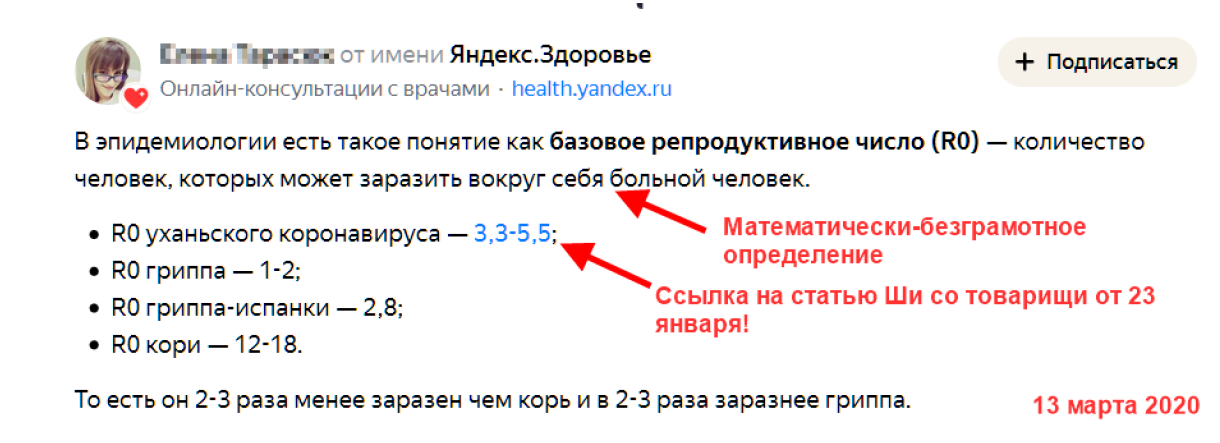
Во-первых, R₀ определено неверно. «Количество человек» можно заразить за какое время? За день, за год, «за один средний чих», за наносекунду? Во-вторых, «можно заразить», где и при каких условиях? На рынке в Ухане или в пустыне Каракум? В толпе на стадионе или в гордом одиночестве дома? В-третьих, совет подают в марте, а ссылка на статью китайских медиков… от 23 января [2]! Напомню, что в ВОЗ про эпидемию в Ухане сообщили 3 января, а первый отчёт по эпидемии вышел лишь 20-го. Двадцать третьего информации было мало, оценка предварительная (камарад Ши так и пишет: preliminary). Товарищу Ши и прочим – наше огромное спасибо за ответственность и оперативность, но уже к середине февраля они же свою раннюю оценку уточнили [1]. Это «от 2.0 до 2.5», а вовсе не «3.3-5.5».

Наконец, в-четвёртых. И это самая главная проблема подобных советов. Если мы говорим об R₀ болезни с любыми симптомами, то речь всегда идёт лишь о скорости распространения болезни в первые дни эпидемии. Именно поэтому там внизу стоит «ноль»! Это «нулевой день» (ну или вблизи нулевого дня), ага. И даже если у вируса в стволе дырка совершенно нет симптомов, и мы о нём не подозреваем, то и тогда R будет меняться от времени и положения вируса на планете.

Поглядим на формулу {7}. Интеграл заразности зависит в основном от биологии вируса и биологии человека; он примерно постоянен. А вот трансмиссивность r зависит от:

• Скорости воспроизводства вируса в организме больных. Скажем, COVID-19 быстрее размножается (поражает больше клеток в единицу времени) у людей пожилых.

• Способа распространения вируса. Скажем, COVID-19 распространяется в основном воздушно-капельным путём.

• Устойчивости вируса во внешней среде.

• Погодных условий. Например, при сильной инсоляции вылетевший наружу коронавирус остаётся опасным считанные секунды. Ультрафиолет корёжит РНК.

• Социальных привычек населения. Принято ли у вас мыть руки после уборной?

• Социальных условий. Есть ли вообще где руки помыть? У вас в городе ватерклозеты или сортиры «с дыркой»?

• Местного этикета. Принято ли в вашей стране целоваться при знакомстве или можно пожать руку? А целоваться со знакомыми при каждой встрече?

• Скученности населения. У вас многоэтажные «человейники» или отдельные коттеджи? Хижины в джунглях? Юрта в степи? А может, рабочие казармы и бараки?

• Вида занятости населения. Офисы или шахты? А может, ювелирные мастерские? Сколько человек трудится вместе? Есть ли профессиональные лёгочные заболевания?

• Может ли заболевание передаваться животными? Насекомыми? В какое время года они активны?

Если спросите у квалифицированного эпидемиолога, он в этот список накидает ещё пару сотен пунктов.

Поэтому R₀ = 2.8 у «испанки» было в среднем по планете тогда. Целую ручку-с. Друг, оставь докурить. Кокаинчику? Один комплект одежды и обуви на лето, второй на зиму, и оба комплекта – на 3-5 лет. Это кому повезло. У кого-то обноски с Каланчёвки. Баня по субботам, раз в неделю. Сортиры с дырками. Рабочие бараки и солдатские казармы. После Первой мировой. Недоедание. Окопы. Походно-полевые бордели на 120 лежачих мест, 360 клиентов в час (кроме шуток). Сколько получился бы R₀ у «испанки» теперь, в 2020? Иншаллах! Уж точно, в Мексике, Иране и КНР были бы разные значения.

Разные значения R₀ могут быть даже в одном городе, но в разных слоях общества. Торговцы с рынка в Ухане имеют немного другие гигиенические привычки и условия труда, чем программист или разработчик печатных плат из того же индустриального мегаполиса. То, что в Китае в среднем получилось 2.0-2.5, совсем не значит, что в среднем по миру будет 2.3. Может быть и больше, и меньше.

Теперь пройдёмся по списку ещё раз. Некоторые параметры, как устойчивость конкретного вируса, там почти фиксированные. Некоторые параметры могут сильно меняться от времени года. Например во времена СССР в июле на диких курортах вокруг Краснодара (на рынке овощи-фрукты, мухи, туалеты именно «дикие») у дизентерии R₀=4.0, а в январе в Норильске у того же возбудителя R₀=0.04. Но главное, есть параметры, которые, по крайней мере в просвещённом обществе, очень легко поменять в сторону уменьшения. При той же эпидемии «испанки» народ довольно быстро научился не пожимать руки и не целовать ручки. Да и на курортах Краснодарского края дизентерия почему-то не косила туристов толпами.

Если у болезни появляются какие-то неприятные симптомы, в дело вступает дистанцирование (distancing), начинающее давить R до значений существенно меньше R₀.

Сделаем наш вирус чуть менее безобидным. Пусть смертей он не вызывает совершенно, но на лице и руках на какое-то время появляется отчётливая фиолетовая сыпь. Ну или болячки на слизистых, как при герпесе. Вероятность появления симптомов определяется фиолетовой кривой φ(t). Зелёная заразность оставлена для сравнения. Пунктиром показана заразность лиц с симптомами (подкрашена малиновым) и лиц без симптомов (серым). Последних может быть до 5%. Про COVID-19 пока точно не известно, но вроде бы на «Алмазной принцессе» именно такой процент давал положительный анализ на вирус при полном отсутствии симптомов.

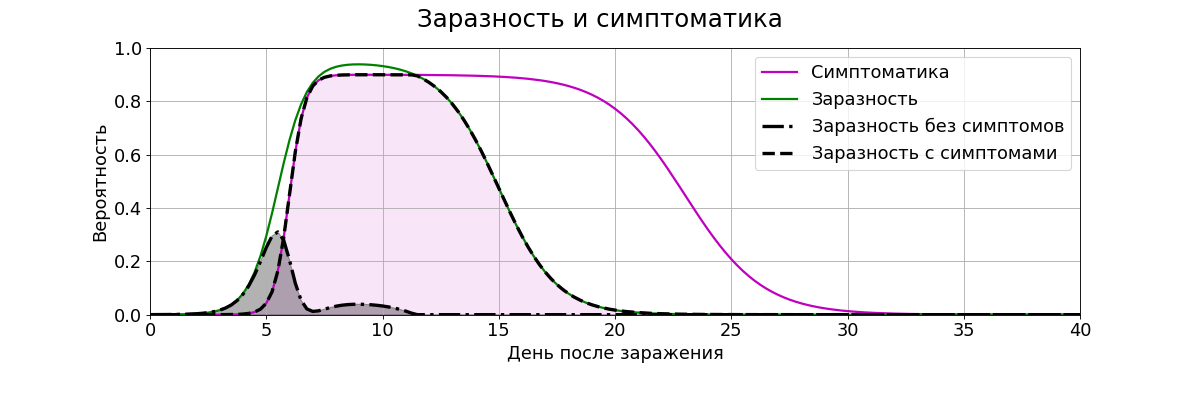
Если человек весь фиолетовый, он вызывает закономерное любопытство. Очень быстро, дней через 5-7, люди замечают, что почти всякий, кто близко с фиолетовыми пообщался, сам становится фиолетовым. Хотя болезнь довольно быстро проходит, и никто не умирает, население быстро сделает определённые выводы, и фиолетовых будут сторониться. При том, сами фиолетовые не будут лишний раз контактировать со здоровыми, стесняясь симптомов заболевания (ну и не желая заражать других). Это и есть дистанцирование.

Незнание микробиологии не помеха. Люди сделали достаточно достоверные выводы про лёгочную форму чумы, туберкулёз и сифилис, не зная ни микроскопа и генетики, ни вообще о бактериях и вирусах. Даже для болезней с огромным инкубационным периодом, типа лепры, во многих обществах было чёткое понимание, что лишний раз с больным лучше не контактировать, а после контакта надо руки помыть. И раздавали прокажённым одновременно и милостыню, и колокольчики.

Для численного примера пока предположим, что для вирусоносителя без симптомов остаётся параметр R_N=R₀, а для явно заболевших – он вдвое ниже, R_S=R₀/2. При этом, ни о какой изоляции заболевших речи нет. Заболев, фиолетовые просто уменьшают количество своих дневных контактов в среднем вдвое: на улицу выходят реже, на работу не ходят, сидят по домам. Выше мы уже договорились, что на 30-й день переболевший полностью не заразен, значит, после исчезновения фиолетовой сыпи может безопасно вернуться в общество. Система уравнений переписывается так:

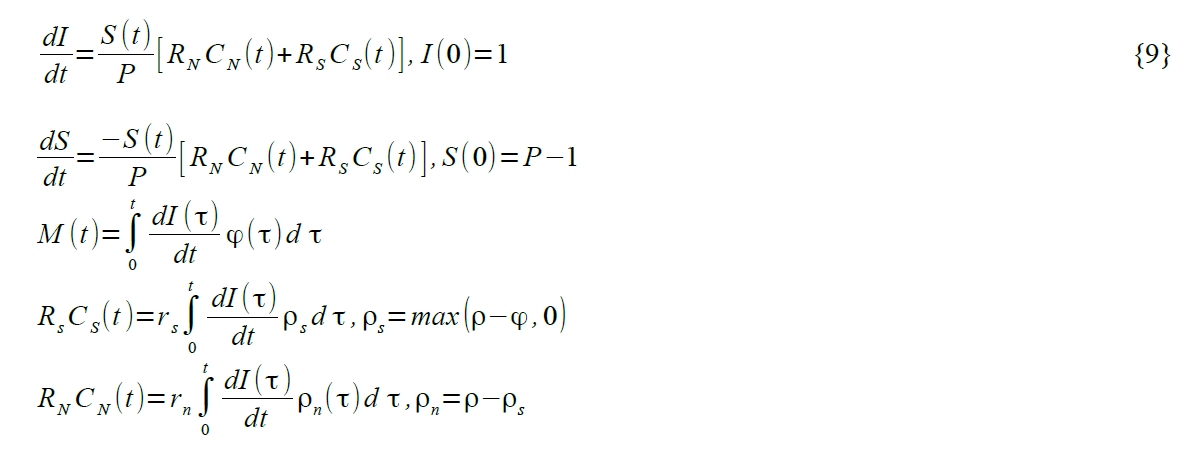
Здесь M(t) – количество явных больных. C_S(t) и C_N(t) – число вирусоносителей с симптомами и вирусоносителей без симптомов, соответственно.

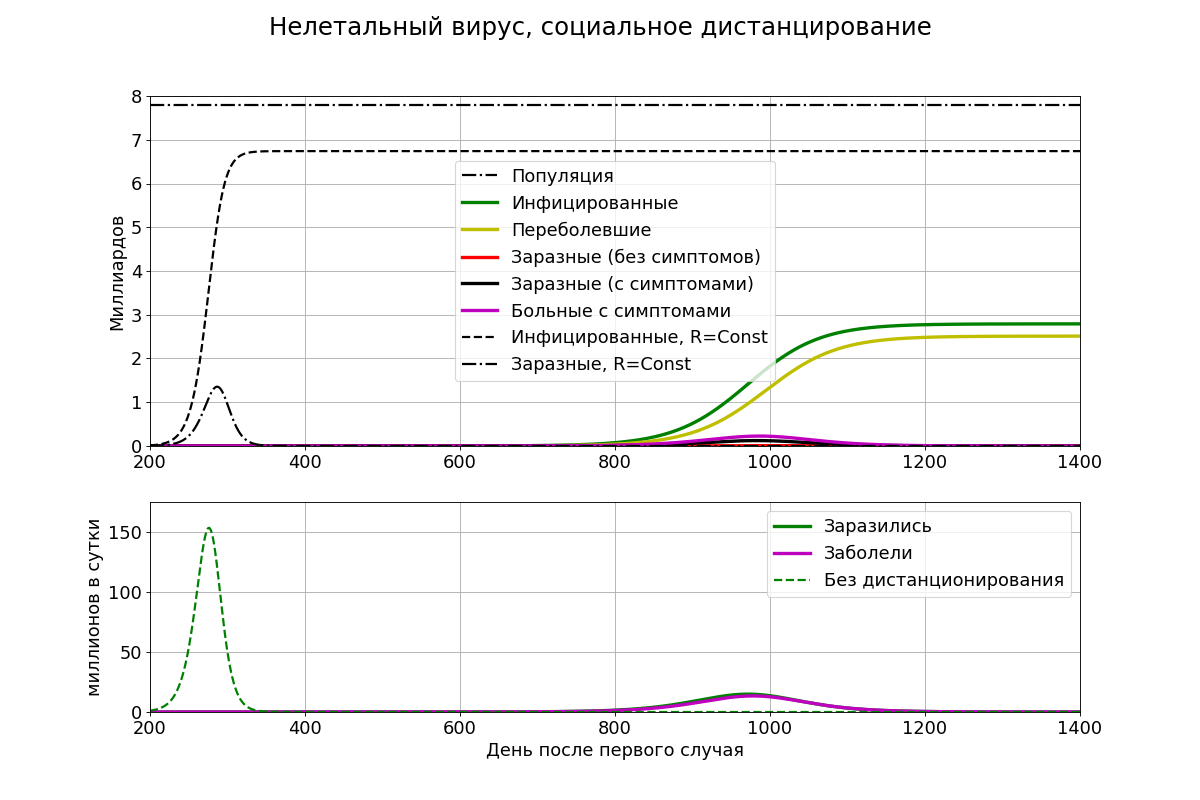
Выбранное нами социальное (применяемое населением добровольно, без армии, полиции, законов, и т.п.) дистанцирование с R_S = 2.30/2 = 1.15 – это даже не полумера; эпидемию тормозит, но не останавливает. А мы такое значение тут специально; если поставить R_s вблизи 1, то миллиардов заражённых никак не получится, график превратится в прямую линию!

В наших, довольно пессимистических, предположениях пик эпидемии откладывается на 600 с лишним дней, а количество инфицированных в конце не превысит 3 миллиардов. Больных с симптомами (откровенно фиолетовых) будет на пике «всего лишь» около 185 млн. Это 185/7'800 = 2.4%. Учитывая, что больные в среднем реже появляются на людях, то пройдясь по улице в самый разгар эпидемии, вы встретите 1-2% «фиолетовых», а вовсе не 90%, как в фильмах из Голливуда. Примерно то же самое происходит при ежегодной пандемии гриппа. По оценкам специалистов Эдинбургского университета [3], ежегодно от гриппа и его осложнений умирают (все значения округлены до ближайшей 1'000):

Ежегодный сезон гриппа длится на Земле примерно 90 дней (некоторые страны начинают и заканчивают раньше, некоторые позже). Во время среднего (не худшего) сезона, на планете умирает от гриппа по 3 человека в минуту. В том числе дети до 5 лет – это известная группа риска. В ещё не полностью закончившийся сезон 2019-2020 года в США инфицированы (штаммом гриппа этого сезона) 36 млн человек (10.9% населения). Из них уже попало в больницы, в том числе с пневмонией, 370 тысяч. И 22 тысячи (0.007% населения США) от гриппа этого года уже умерли. Опять-таки, включая детей и подростков. Детей вы этом году почему-то было пропорционально больше, чем бывает в «среднюю» эпидемию гриппа.

Просто для сравнения, в Африке от ВИЧ/СПИД умирает ежегодно около 1.0 млн, там же от малярии от 300 до 400 или даже 450 тысяч. От ВИЧ одна смерть каждые 35 секунд.

При этом об умерших от коронавируса COVID-19 150 американцах (0.00005% населения США) в американской же прессе стоит жуткий вой и паника. Именно об американцах, даже мексиканцы и канадцы в среднем американские СМИ мало волнуют, не говоря уж о китайцах. Про КНР средний американец только знает, что «пришло оттуда», а про Европу и Иран – что «пришло туда». Начитавшись и насмотревшись СМИ, средний американец бежит в супермаркет зачищать полки от туалетной бумаги или стоит в очереди в оружейный магазин. При этом, вероятно, может заразиться, а если сам уже заразен – то заразить окружающих. Про 22'000 умерших в США от гриппа журнашлюхи просто «забыли упомянуть, разве это важно?»

Опыт гриппа показывает, что социальное дистанцирование может сработать только если заболевание представляется в глазах публики достаточно опасным. В случае гриппа, например, это не так. Врачи призывают-призывают, а народ забивает-забивает. В США в среднем за год умирает по 35 тысяч не потому, что медицины в США совсем уж нет, а потому, что контакты больных со здоровыми почти никак не ограничены! Медики просят при насморке и головной боли сидеть дома, а заболевший принимает какой-нибудь «геданол» – симптомы исчезают часов на 6-8, точно как в рекламе, – и бежит на работу. А школьники сначала к врачу, потом в кино или на дискотеку. А поскольку «геданол» уже принят, то и здоровенькие определить больных/заразных никак не могут. Это в нашей задачке (ствол с дырочкой) все больные фиолетовые. А в жизни-то обычные.

Продолжение следует.

Примечание:

Здесь ни в коем случае не написано, что COVID-19 -- это чепуха, и что его нету. Если вы так поняли, что 3 млрд инфицированных -- это чепуха, то это ваши проблемы. Но при всём при этом, насчёт коронавируса паниковать не надо. Болезнь неприятная, относиться надо серьёзно. Но не паниковать. "Убивает не сибирская язва, но паника" - это из старого армейского наставления по борьбе с оными обеими.

Дистанцируйтесь заранее. Не посещайте массовые мероприятия, в том числе в храмах. Не слушайте, что говорят про средства индивидуальной защиты некоторые доктора. Носите маски. Носите очки (лучше солнцезащитные строительные). Китайцы, корейцы, вьетнамцы, сингапурцы (сам видел) вам улыбаются и машут, ВОЗ тоже. Правда, как улыбаются, почему-то не видно. Ну, вы поняли.

Если слегка простудились, железобетонно посидите дома. Почти наверняка у вас не COVID-19, а если даже и он, то будет лёгкий, как простуда. Однако заражаться тем, что вы там подцепили, людям лишний раз ни к чему, а вам ни к чему послевирусные осложнения (пневмококк коварнее). Кстати, эпидемия гриппа 2019-20 ещё не везде закончилась.

Человечество пережило таких "последних, ужасных, катастрофических пандемий" много сотен. Последняя была в 2009, притом родственник "испанки" грипп А/H1N1 убивал больше не старых, а молодых. Убил более 500 тысяч. (Да, я этим гриппом переболел. Нет, не дождётесь.) И истерию COVID-19 мир переживёт, слегка улыбнувшись.

Здоровья.

Ссылки:

[1] Report of the WHO-China Joint Mission on Coronavirus Disease 2019 (COVID-19), WHO, https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mis...

[2] Shi Zhao et al, Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020 doi: 10.1101/2020.01.23.916395 (не проходило рецензирования)

[3] J.Pager et al, Global mortality associated with seasonal influenza epidemics. Dec 2019. doi: 10.7189/jogh.09.020421

[4] https://www.cdc.gov/flu/about/burden/index.html

[5] Rudragouda Channappanavar, Jincun Zhao, and Stanley Perlman, T-cell-mediated immune response to respiratory coronaviruses,doi:10.1007/s12026-014-8534-z.