Данная заметка является продолжением публикации Аналогии экономики с термодинамикой и механикой,
при обсуждении которой было высказано следующее пожелание "К сожалению,
данная заметка уж очень лаконична. Возможно, вам стоит посвятить этому
вопросу некую серию заметок-лекций, создав раздел под всю серию.
Многим людям такой формат, с возможностью обсуждения с автором, будет
интереснее, чем просто учебник." Имеется ввиду учебник: И.Г.Царев Математика и физика для экономистов.
Такая серия заметок подготовлена и будет публиковаться в общем разделе Аналогии экономики с термодинамикой и механикой.
Исследуя действительность, человек неоднократно имел возможность
убедиться, что природа бесконечно сложна. Поэтому, не обладая
божественной мудростью для постижения этой бесконечности, человек
стремиться объяснить себе мир попроще. Общепринятым представлением о
мире является понятие «системы». Систему представляют как совокупность
неких объектов, которые как-то связаны между собой. Эти связи мысленно
представляют как поле неких сил.
Далее человеку требуется описать эту систему на каком-то языке.
Исторически первый способ описания при помощи слов получил название
«философия». И лишь много позднее был придуман значительно более
формализованный язык описания – при помощи математической символики.
Этот способ описания природы получил название «наука».
Можно сказать, что «крестным отцом» науки был астроном Галлей,
который убедил своего приятеля Ньютона решить одну (!) задачу о
притяжении тел. Точнее, идею решения этой задачи Ньютону предложил Гук,
предположив в 1679 году, что притяжение обратно пропорционально квадрату
расстояния, и при этом тела должны двигаться по эллипсам. Галлей убедил
Ньютона эту задачу решить. Немного повредничав, Ньютон за задачу
взялся, исследовал закон движения, убедился, что действительно
получаются эллиптические орбиты, доказал, что, и обратно, из закона
Кеплера об эллиптичности орбит следует и закон обратных квадратов. Для
того чтобы все это как следует оформить и изложить в доступном виде, ему
потребовалось сформулировать основные принципы, относящиеся к общим
понятиям, таким как масса, сила, ускорение. Так появились знаменитые
«три закона Ньютона», на которые сам Ньютон не претендовал, так как они
были открыты раньше.
В результате Ньютон написал работу с подробным изложением своих
результатов под названием «Математические начала натуральной философии» и
прислал её Лондонскому королевскому обществу 28 апреля 1686 года. Эту
дату можно считать днем рождения «науки», в которую превратилась
«философия», поскольку, как значительно позднее сказал Иммануил наш
Кант: «Наука лишь постольку наука, поскольку в нее входит математика».
«Натуральной философией» тогда называлась область знания, которую сейчас
называют «физикой». Само собой, что математика появилась задолго до
Ньютона, а заслугой Ньютона является отыскание аналитического решения
одной(!) конкретной задачи, что является большой удачей. Как обычно
бывает, рациональный и лаконичный язык математической символики имеет
свои ограничения. За примерно пятьсот лет научных изысканий примеры
аналитического решения задач крайне редки и являются жемчужинами в
безбрежном океане знаний. Однако эти немногие примеры дают очень многое
для понимания окружающего мира, и на них построено все здание
современной науки.
Таким образом, способ описания природы под названием «наука» выглядит
следующим образом. Исследователь наблюдает некое реальное явление и
воображает его в виде некой «системы». Для этой системы он выделяет
некие «важные», по его мнению, свойства, а остальные «несущественные»
опускает. Далее он пытается описать воображаемую в своей голове систему
на математическом языке. «Объекты», «свойства» или какие-то другие
«величины» в этой модели исследователь называет «функциями», а связи
между ними описывает в виде «уравнений». Результат этой процедуры в
случае удачи называется «математическая модель». Общеизвестно, что когда
удается подобрать удачную математическую модель для описания
какого-либо реального процесса, то полученное описание в свою очередь
позволяет по-новому взглянуть на изучаемое явление, обратить внимание на
те стороны процесса, которые до этого находились в тени.
Чаще всего исследователь просто проводит «анализ» модели, например,
при помощи приближенного вычисления функций, разложенных в «ряд». Этот
метод изобрел также Исаак Ньютон, и считал его самым своим важным
открытием, важнее, чем открытый закон всемирного тяготения и придуманное
им дифференциальное и интегральное исчисление, чтобы этот закон
описать. Если так называемый «анализ» математической модели приводит к
результату, хотя бы приблизительно похожему на наблюдаемое явление
природы, исследователь заявляет, что он без сомнения гений, открывший
новый закон природы, и скромно ждет вручения нобелевской премии. Если же
исследователь умудряется придумать такую модель, которая имеет
аналитическое решение (не численное, а в виде конкретных формул), да еще
и вычисляет это решение в явном виде, то нобелевской премии ему уже
мало. Он, независимо от мнения окружающих коллег, считает себя столпом
науки (основанием, на которое опирается здание науки) и скромно ждет
вечной славы и поклонения.
Насколько найденные решения являются правильными? А неизвестно. Так
как математическая модель предполагает учитывать только «важные»
свойства бесконечно сложного природного объекта и опускать рассмотрение
«несущественных» свойств, так как все измерения неизбежно дают ошибку,
то никакая математическая модель не дает абсолютного совпадения с
результатом эксперимента. В какой-то момент большинство научного
сообщества решает, что уже поставлено достаточное количество
экспериментов и полученные результаты имеют не очень большой разброс
(дисперсию). Если математическая модель дает результаты, близкие к
результату эксперимента, то большинство научного сообщества может
решить, что «научная гипотеза» стала «научной теорией». Вот и всё.
Никаких методов, которые могут «абсолютно точно» подтвердить истинность
выбранной математической модели не существует.
Если читатель считает, что автор этих слов «слишком много на себя
берет», а законы природы установлены с абсолютной и объективной
точностью, то я обращусь к мнению такого известного нобелевского
лауреата, гения и столпа науки, каким является Л.Д.Ландау. На стр. 10
Части 1 учебника «Статистической физики» этот признанный корифей написал
буквально следующее: «Среди физиков довольно широко распространено
заблуждение, что статистическая физика является наименее обоснованной
областью теоретической физики. При этом обычно ссылаются на то, что
некоторые выводы статистики доказываются не строго математически, и
забывают, что все другие (курсив мой) области теоретической
физики содержат столь же нестрогие доказательства, что, однако, не
рассматривается как признак недостаточной обоснованности данных
разделов». Как говориться, ни убавить, ни прибавить.
Так Великий Триумф Закона Всемирного Тяготения Ньютона наступил 13
марта 1759 года когда на небе засияла комета, предсказанная на основании
этого закона его приятелем астрономом Галлеем. Правда комета «опоздала»
на 618 дней, так как Галлей не учел в расчетах «возмущения, вызванные
притяжением Юпитера и Сатурна». Но это уже было неважно. Галлей и
особенно Ньютон с той поры стали признанными гениями, а Ньютон еще и
столпом науки. Комету немедленно назвали «кометой Галлея».
А как же Гук, спросите вы, который предложил Ньютону идею решения
этой задачи и предположил готовый ответ, что «притяжение обратно
пропорционально квадрату расстояния, и при этом тела должны двигаться по
эллипсам»? Ньютон очень сильно нервничал по этому поводу. Он не
соглашался возглавить Королевское общество при жизни Гука. Только после
смерти Гука, в 1703 году Ньютон согласился занять пост президента
Королевского общества. И одним из первых актов Ньютона на этом посту
было уничтожение всех инструментов умершего Гука, а также его бумаг и
портретов. Так что теперь Королевское общество располагает портретами
всех своих членов, кроме Гука. Ни одного изображения Гука, который был
членом, куратором и секретарем Королевского общества, не сохранилось.
Причем, не следует все понимать так, что Гук открыл закон всемирного
тяготения, а Ньютон этот закон украл. Каждый выполнил свою часть работы.
Просто обязанности куратора Королевского общества были весьма
нелегкими. Согласно контракту, Гук должен был на каждом еженедельном
заседании демонстрировать три или четыре опыта, доказывающих новые
законы природы. Разумеется, в контракт не входило условие, что все
демонстрируемые законы должны быть изобретены им самим. Поэтому Гук по
обязанности интересовался всеми естественнонаучными открытиями других,
но и самому ему тоже приходилось делать открытия. К концу жизни он
насчитывал 500 открытых им законов. Надо сказать, что эти законы
составляют основу современной науки. Очень многие из них более или менее
параллельно были открыты другими учеными. В итоге закон упругости носит
имя Гука, а остальные его открытия носят другие имена. В силу контракта
у Гука никогда не было достаточно времени, чтобы остановиться на
каком-то своем открытии и подробно его развить, и иногда он в спешке
делал утверждения, которые не мог аккуратно и строго математически
обосновать.
В своей переписке с Галлеем Ньютон, отвечая на просьбу Галлея
упомянуть Гука, написал замечательную фразу, раскрывающую его мнение о
различии между математиками и физиками. Себя Ньютон считал математиком, а
Гука считал физиком: «Математики, которые все открывают, все
устанавливают и все доказывают, должны довольствоваться ролью сухих
вычислителей и чернорабочих. Другой же, который ничего не может
доказать, а только на все претендует и все хватает на лету, уносит всю
славу как своих предшественников, так и своих последователей. … И вот я
должен признать теперь, что я все получил от него, а что я сам всего
только подсчитал, доказал и выполнил всю работу вьючного животного по
изобретениям этого великого человека».
Для того, чтобы продемонстрировать, как используется изложенный метод
научного познания в современной экономике, представим теперь, что
Ньютон был бы не математиком, а экономистом. Вместо того, чтобы
придумать подходящую математическую модель и найти её решение в
аналитическом виде для всех возможных случаев, т.е. вместо того, что
сделал математик Ньютон, экономист Ньютон мог бы по примеру Галилея для
начала кидать ядра с Пизанской башни и замерять разные параметры. Затем
кидать их вверх под разными углами. Потом кидать предметы разного веса и
с разной скоростью. Далее можно было бы учитывать влияние воздуха,
ветра, времени суток и года, вращения Земли (силы Кориолиса), влияния
Луны и т.д. Можно было бы строить различные статистические
последовательности, ряды, определять коэффициенты корреляции и
изобретать различные математические модели с различными параметрами для
анализа этих статистических последовательностей. И применять их на
практике. Этим можно заниматься всю жизнь. Примерно этим и заняты те
современные экономисты, которые применяют математику. Прочие экономисты
заняты «философией».
Естественно, что была предпринята попытка создать такую
математическую модель, которую можно было бы применить для какого-угодно
процесса. Усилиями большой группы исследователей, среди которых
наиболее известны Эйлер, Лагранж и Гамильтон, была придумана некая, по
общему мнению, универсальная математическая модель, которая получила
общепринятое название «динамическая система». Данная модель представляет
любое наблюдаемое явление в виде некой динамической (движущейся)
системы обыкновенных дифференциальных уравнений. Система состоит
из «параметров», «координат» и «функций». Самым известным параметром
является время t. Хотя система может содержать и какие-то
другие параметры, в том числе некие постоянные величины, от которых
зависит поведение системы.
Координаты не являются привычными нам координатами в привычном нам
пространстве. Точнее так, пространство динамической системы может
содержать привычные нам пространственные координаты, но не обязательно
только их, и даже не обязательно их. Координат должно быть столько,
чтобы полностью определить текущее состояние динамической системы. В
случае задачи Ньютона для полного описания состояния движущейся частицы
или маленького тела (материальной точки) достаточно шести координат:
во-первых, трех компонент вектора координаты q, а во-вторых, трех компонент вектора скорости (по версии Эйлера-Лагранжа) или трех компонент вектора импульса p (по версии Гамильтона). Соответственно, для k точек необходимо, по версии Гамильтона, 2n координат:
(p,q)=p1,...,pn,q1,…,qn, где n=3k.
Все эти координаты зависят от параметра t. Однако в некоторых «неавтономных» системах время t может выступать в качестве независимой координаты. Координаты должны
быть «существенны», т.е. они должны полностью описывать поведение
системы. Кроме того, координаты должны быть «независимы», т.е. те
координаты, которые могут быть выражены через другие координаты, должны
быть отброшены.
Функциями называют величины, которые входят в уравнения динамической
системы. Те функции, которые удовлетворяют дифференциальным уравнениям
динамической системы, называются её «решением» или «интегралом
движения», а процедура отыскания этих решений называется
«интегрированием» системы. Эту задачу ни Ньютон, ни многочисленные
последователи не смогли решить аналитически даже для случая трех тел,
но, тем не менее, Эйлер, Лагранж и Гамильтон без сомнения являются
гениями.
Если мы теперь систему из нескольких точек, которые движутся в
привычном нам пространстве представим для удобства рассмотрения в виде
одной (!) точки, которая имеет 2n координат, то с математической точки
зрения система совершенно не изменится. В этом случае каждый конкретный
набор значений координат задает «состояние» или «фазу» системы в
2n-мерном пространстве, которое называется «фазовым пространством».
Изменение импульсов и координат реальных частиц в реальном пространстве
вызывает соответствующее изменение координат нашей динамической системы,
состоящей из одной точки, в фазовом пространстве (или пространстве
состояний системы). Если же некоторые точки в реальном пространстве
«связаны», например, две точки связаны невесомым стержнем или нитью, то
одна или несколько координат фазового пространства также окажутся
«связанными» или «зависимыми». Это означает, что данные координаты могут
быть выражены через «независимые» координаты. Таким образом, число
независимых координат фазового пространства будет меньше, чем 2n. В
результате фазовое пространство может представлять собой не привычное
нам бесконечное пространство, а некую «поверхность». Чтобы это лучше это
понять, можно представить в трехмерном пространстве некую двумерную
фигуру, например, цилиндр или сферу, которая получилась в результате
«связи». Такие пространства «со связями» называют конфигурационными
пространствами, а также многообразиями (хотя, вообще говоря, эти понятия
не тождественны). Установлено, что для динамической системы мы всегда
будем иметь «двойной набор» координат. Половину будут составлять
«условные координаты», а другую половину «условные импульсы». Таким
образом, «связывание» пространственной координаты приводит к
«связыванию» соответствующего импульса. Такие многообразия с двойными
(четными) наборами координат, называются симплектическими многообразиями.
Стало быть, динамической системой называется система обыкновенных
дифференциальных уравнений, заданных на симплектическом многообразии.
Геометрический смысл дифференцирования состоит в замене математического
объекта другим, более простым объектом, а именно исследуемой n-мерная
поверхность в окрестности точки дифференцирования заменяется касательной
n-мерной плоскостью, которую намного проще исследовать. Например,
рассмотрение поведения кривой в окрестности точки дифференцирования
заменяется рассмотрением прямой, которая касается исходной кривой в
точке дифференцирования, двумерная поверхность заменяется касательной
плоскостью, а n-мерное пространство заменяется касательным пространством
такой же размерности. Если исследуемый математический объект имеет
изломы или разрывы в каких-то точках, то в этих точках невозможно
построить касательную плоскость. Поэтому говорят, что в таких точках
объект не дифференцируем. Напротив, дифференцируемые во всех своих
точках объекты называются «гладкими» или дифференцируемыми достаточное
число раз.
Движение нашей точки (системы) от одной фазы (состояния) к другой
образует «фазовую траекторию» или «фазовую кривую» на гладком
симплектическом многообразии. В обычном пространстве траектории движения
могут пересекаться, так как из каждой точки обычного пространства может
«торчать» множество векторов импульса, направленных в разные стороны. В
фазовом пространстве из каждой точки может «торчать» или, как культурно
выражаются математики, к каждой точке фазового пространства может быть
отнесен только один вектор фазовой скорости. Так как из каждой точки
торчит только один вектор, то фазовые траектории никогда не
пересекаются. Это означает, что каждая точка фазового пространства
однозначно задает состояние исследуемой системы и направление
дальнейшего движения. Например, в точке равновесия фазовая траектория
представляет собой просто точку.
Совокупность всех векторов фазовой скорости образует «векторное
поле», которое задано выбранной системой обыкновенных дифференциальных
уравнений.
Динамическая система Гамильтона имеет следующий общий вид:

Здесь функция H, называемая Гамильтонианом, является
«решением» или «первым интегралом» системы, а второе и третье уравнения
являются «векторным полем фазовых скоростей».
Чтобы выписать уравнения для системы Лагранжа, применим так
называемое преобразование Лежандра, которое является вспомогательным
математическим приемом:
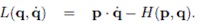
Здесь L называется функцией Лагранжа или лагранжианом. Система Лагранжа имеет вид:
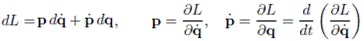
Второе и третье уравнения носят название уравнений Эйлера-Лагранжа.
Если функция H полностью определена набором координат (p,q)=p1,...,pn,q1,…,qn, то dH является «полным дифференциалом» системы, и её можно теоретически
вычислить или «восстановить первообразную по полному дифференциалу». В
этом случае динамическая система называется «автономной». Если же
функция H зависит еще и от t «явно», т.е. в виде
независимой координаты, то такой первый интеграл системы называется
«непостоянным», а динамическая система называется «неавтономной». В этом
случае L также зависит от времени «явно», приведенные выше выражения dH и dL для этих функций не являются полными дифференциалами, а фазовое пространство «расширяется» еще на одну независимую координату t и называется «расширенным 2n+1 мерным фазовым пространством».
В этом случае преобразование Лежандра будет иметь вид:
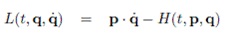
причем очевидно, что
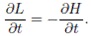
Тогда можно выбрать такую функцию S(t,q), что
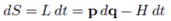
Причем dS является полным дифференциалом функции S.
Этот полный дифференциал задает фазовые траектории в расширенном
фазовом пространстве. Исторически он называется интегральным инвариантом
Пуанкаре-Картана. В результате запишем:
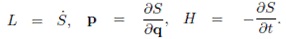
Вспомогательная функция S исторически называется
«производящей функцией» или «действием». Специально для любителей волн
можно выписать так называемое «волновое уравнение»:
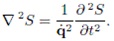
Однако для механической системы (а впоследствии и для других
природных систем) был обнаружен один замечательный закон природы.
Экспериментально установлено, что если описать природный процесс при
помощи системы Гамильтона, то переход системы из одного состояния в
другое (траектория системы в расширенном фазовом пространстве) всегда
происходит по кратчайшему пути между двумя точками. Кратчайший путь
между двумя точками играет роль прямой на многообразии и называется
«геодезической линией». На плоскости геодезические линии суть прямые, на
цилиндре – винтовые линии, на сфере – окружности, центры которых
совпадают с центром сферы. В общем случае длина пути есть некий скаляр,
который может быть вычислен как интеграл по времени от интегрального
инварианта Пуанкаре-Картана:
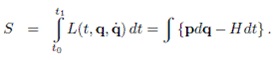
Условием того, что величина S будет минимальной, т.е. что
движение будет происходить по геодезической линии, является выполнение
уравнений Эйлера-Лагранжа. В механике это обязательное движение системы
по геодезической линии было названо «принципом наименьшего действия
Гамильтона». С точки зрения принципа наименьшего действия природа
достигает своей цели прямейшим путем, следовательно, с наименьшей
затратой средств. Поэтому более удачен был бы термин «принцип наименьшей
затраты средств, при наибольшем действии». Но после того как термин
«действие» для функции S был санкционирован Гельмгольцем и Планком, всякая замена его другим термином была бы бесперспективной.
Простейший пример наикратчайшей траектории – распространение луча
света по прямой, но наикратчайшая траектория, это не обязательно прямая
линия. Рассмотрим брахистохрону – кривую скорейшего спуска, например,
при стекании воды с холма. Задача о её нахождении была поставлена в 1696
году Иоганном Бернулли. Одно из решений дано в знаменитом учебнике
Лопиталя. В однородном поле тяжести брахистохрона представляет собой
перевёрнутую циклоиду – кривую, которую описывает относительно земли
точка на ободе катящегося колеса. Верхняя точка траектории есть точка
возврата циклоиды (точка касания земли).
Отыскание решения динамической системы в аналитическом виде, т.е.
запись решения через так называемые элементарные функции (степенная,
показательная, тригонометрические и т.д.) исторически называется
вычислением «в квадратурах». В общем виде эта задача для динамической
системы не поддается средствам современной математики и, по-видимому,
неразрешима. Каждое найденное решение, как мы уже знаем, является
отысканной с невероятным трудом и талантом «жемчужиной знания».
Если применить динамическую систему Гамильтона (Лагранжа) для
частного случая (!) «аналитической механики», мы получим, что функция H(p,q), называемая Гамильтонианом, является полной энергией системы E. Изменение полной энергии dH – слева, равно изменению кинетической и потенциальной энергии – справа.
Таким образом, первое уравнение в приведенной выше записи уравнений
Гамильтона отражает закон сохранения энергии механической системы.
Можно предположить, что закон сохранения энергии лидирует по числу
экспериментов, поставленных для его подтверждения или опровержения.
Большинство научной общественности убеждено, что этот закон давно и
надежно установлен. Псевдонаучное меньшинство не оставляет попыток
доказать обратное. В осенне-весенний период число таких попыток
увеличивается.
Если мы проделаем известные в аналитической механике преобразования, то получим:

Рассмотрим важный частный случай динамической системы, когда её
удается проинтегрировать в квадратурах, а именно колебательную
динамическую систему. При этом замкнутые фазовые кривые задают
периодическое (циклическое) движение (процесс) или колебание. Системы,
совершающие колебания, называются осцилляторами. Время полного цикла
колебания T называется «периодом». Частота колебания ν –
обратная периоду величина и характеристика периодического процесса,
равная числу полных циклов, совершенных за единицу времени, выражается
формулой:
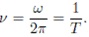
Величина ω называется круговая частота.
Если представить периодическое движение в 2n мерном фазовом
пространстве, то соответствующее симплектическое многообразие будет
представлять собой n-мерный тор. В процессе движения фазовая траектория
остается все время на торе и называется обмоткой тора. Если частота
непостоянна, но меняется достаточно медленно, то фазовые кривые при этом
незамкнутые и сложным образом навиваются сами на себя, а движение
называется условно-периодическим или квазипериодическим. Решение такой
системы можно отыскать путем удачной замены координат (p, q) на так называемые координаты действие-угол:
(I, φ) = (I1,…,In,φ1,…,φn).
При этом координаты действие I получают вычислением производящей функции (действия) при обходе замкнутой кривой (цикла).
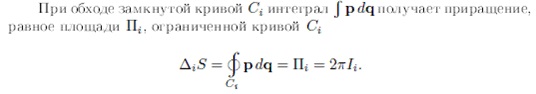
При этом динамическая система Гамильтона будет иметь вид:
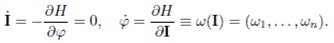
Эти уравнения немедленно интегрируются:
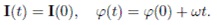












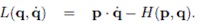
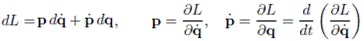
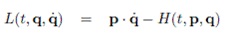
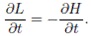
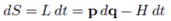
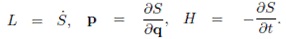
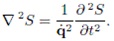
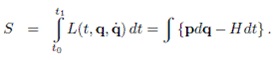

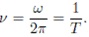
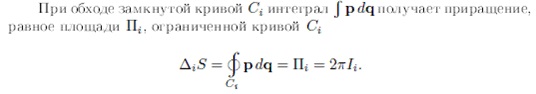
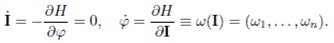
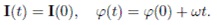


Статус:
Группа: Эксперт
публикаций 0
комментариев 1057
Рейтинг поста:
Я так и подозревал, что Пифагор - это выдумка...
Как же жили древние египтяне и ацтеки без Ньютоновского математического аппарата, да еще умудрились пирамиды построить? Чудеса.
Статус:
Группа: Посетители
публикаций 0
комментариев 219
Рейтинг поста: