Поль Дирак— человек, открывший Антимир

Содержание:

 

1. ПОЛЬ  ДИРАК — МОЛОДЫЕ   ГОДЫ

2. ПОЛЬ ДИРАК — ПРИНЦИПЫ ЛИЧНОСТИ

3. КВАНТОВАЯ  МЕХАНИКА  ПЕРЕД  ОТКРЫТИЕМ  АНТИМИРА

4. «НО ВЕДЬ ЭТА ПРОБЛЕМА УЖЕ РЕШЕНА КЛЕЙНОМ?»

5. УРАВНЕНИЕ  ДИРАКА

6. ОТРИЦАТЕЛЬНЫЕ  ЭНЕРГИИ,  «ОСЛИНЫЕ ЭЛЕКТРОНЫ», ТЕОРИЯ   ДЫРОК И   ПУЗЫРЕК  С ЛЕКАРСТВАМИ

7. ЧТО   ДАЛО   ФИЗИКЕ  ОТКРЫТИЕ  ПОЗИТРОНА?

 

 

Любой физик еще с университетской скамьи знает об уравнении Дирака, о дельта-функции Дирака, о статистике Ферми—Дирака, о монополе Дира­ка. Но Дирак велик и интересен не только как ученый, но и как личность. Есть прекрасное высказывание Эйн­штейна о том, что «моральные качества замечательного человека имеют большее значение для его поколения, чем чисто интеллектуальные достижения. Эти последние сами зависят от величия духа, величия, которое обычно оста­ется неизвестным».

 

1. ПОЛЬ  ДИРАК — МОЛОДЫЕ   ГОДЫ

Поль Адриен Морис Дирак, второй из трех детей Чарльза Адриена Ладисласа Дирака и Флоренс Ханны Холтен, родился 8 августа 1902 года в Бристоле. Его отец, швейцарец по происхождению, приехал в Англию еще совсем молодым и там женился. Он преподавал французский язык, причем в той же самой школе, где учился Поль. Это обстоятельство создавало дополнитель­ные трудности. Естественно, отец Дирака хотел, чтобы его дети знали французский язык лучше других учени­ков. Поэтому он установил дома жесткое правило — все разговоры с ним дети должны были вести только на французском. Однако благие педагогические намерения зачастую приводят к совершенно неожиданным результа­там. Так и в этом случае. В ответ на требования отца Поль стал дома преимущественно молчать. Биографы Дирака считают, что именно таким образом уже в детст­ве у него выработалась привычка к сдержанности и не­многословию. Остается только поблагодарить судьбу за то, что отец Дирака преподавал французский, а не фи­зику или математику. Вполне возможно, что, насаждая у себя дома культ этих наук, он смог бы так же успешно отбить всякий интерес Поля и к естествознанию.

Во время обучения в университете он специализиро­вался в электротехнике. Но главным любимым занятием его и в школе, и в колледже была математика. Матема­тические способности обнаружились у него довольно рано, и уже школьные учителя были удивлены его реше­нием стать инженером. Однако, как признается Дирак, этот выбор был обусловлен просто тем, что он не пред­ставлял себе, как можно заработать на жизнь, занима­ясь чистой математикой.

Вообще говоря, судьба будущего нобелевского лауре­ата складывалась в молодости довольно сложно. После окончания в 1921 году Бристольского университета он хотел продолжить свое образование в одном из крупней­ших научных центров Англии — Кембридже. Однако стипендии, которую он получил по результатам экзамена, 70 фунтов стерлингов в год, явно не хватало для безбед­ного существования. Дираку пришлось вернуться в Бри­столь. Он стал усиленно искать работу по своей специ­альности — инженера-электротехника. Но все его попытки не увенчались успехом — в Англии в то время царила жестокая экономическая депрессия. Дирака сильно выру­чило предложение математического факультета Брис­тольского университета, который предоставил ему право изучать математику, освободив от платы за обучение.

Интересно, что вместе с Дираком училась еще только одна студентка. Она решила изучать прикладную мате­матику, и Дирак, чтобы не затруднять преподавателей чтением разных курсов лекций, присоединился к ней.

Через два года материальное положение Дирака улуч­шилось. Он смог получить сразу две стипендии: дота­цию от министерства научных и промышленных исследований и так называемую стипендию выставки 1851 года. Последняя была самой большой стипендией, которую мо­жет получить в Англии молодой ученый. Она обеспечи­вала возможность заниматься наукой в течение двух-трех лет. Так что у Дирака теперь были условия, чтобы осуществить свою давнюю мечту—продолжить образо­вание в Кембридже.

В Кембридже 20—30-х годов работала целая плеяда выдающихся физиков. Дирак еще застал легендарного Дж. Дж. Томсона — первооткрывателя электрона. Пре­емником Томсона на посту директора Кавендишской ла­боратории был знаменитый Эрнест Резерфорд. Под руко­водством Резерфорда работали такие замечательные физики-экспериментаторы, как П. Л. Капица, П. Блэкетт, Дж. Чедвик, Г. Гейгер, Э. Марсден, Дж. Кокрофт, М. Олифант — что ни имя, то целая страница в истории физики. Не менее представителен список теоретиков, ра­ботавших в то время в Кембридже. Среди них были та­кие известные ученые, как Дж. Лармор, Р. Фаулер, Э. Каннингэм, Дж. Леннард-Джонс. В Кембридже рабо­тали также выдающиеся астрофизики и космологя А. Эддингтон и Э. Милн.

Так что Дирак сразу попал в благоприятную атмосфе­ру переднего края науки и получил возможность изучать физику под руководством первоклассных ученых. Напри­мер, курс по магнетизму Дираку читал П. Л. Капица. На­учным руководителем Дирака был один из основных кем­бриджских теоретиков Р. Фаулер, а когда Фаулер уехал в Копенгаген поработать в институте Нильса Бора, то научными исследованиями Дирака руководил Э. Милн.

Надо сказать, что Дирак был довольно своеобразным студентом. На лекциях он старался понять лишь основ­ные идеи. Весь остальной материал Дирак разбирал са­мостоятельно, по книгам и оригинальным статьям. Зачастую в ходе такой работы Дирак находил более кор­ректные доказательства или новые пути для решения не­которых хорошо известных и широко обсуждавшихся проблем. Так родились его первые научные работы. От­метим, что только тема для самой первой статьи была предложена Дираку его научным руководителем. В даль­нейшем он всегда выбирал предмет исследования самос­тоятельно.

Два слова о «светской» жизни Дирака. Только два слова — просто потому, что практически никакой «свет­ской» жизни молодой Дирак не вел. В театре не бывал, в гости ходил очень редко, мало читал беллетристику. Единственным его развлечением были воскресные про­гулки. Обычно он брал еду с собой и уходил на целый день. На таких прогулках он не старался специально думать о науке, но подчас очень интересные мысли при­ходили как раз во время воскресных походов.

Вообще говоря, научная карьера Дирака была бле­стящей и стремительной. В 24 года он защищает диссер­тацию, а спустя четыре года становится членом Королев­ского общества (аналог нашей Академии наук). В 30 лет он стал профессором и в течение 36 лет возглавлял зна­менитую Лукасианскую кафедру в Кембридже. Этот пост в свое время занимал Исаак Ньютон. В 31 год Дирак по­лучил Нобелевскую премию.

 

2. ПОЛЬ ДИРАК — ПРИНЦИПЫ ЛИЧНОСТИ

На мой взгляд, основная черта характера Дирака — это сочетание высокого профессионализма с безгранич­ным удивлением перед окружающим миром.

Я не случайно поставил на первое место профессиона­лизм. Казалось бы, очевидно, что выдающийся ученый должен быть прежде всего мастером своего дела. Однако еще бытует мнение, что владение научным аппаратом — это одно, а вот свежую и нетривиальную идею может вы­двинуть любой человек, знакомый лишь с основными прин­ципами науки. Один мой знакомый, ученик известного у нас академика, показывал мне груду писем, которые приходят на имя этого академика, с предложениями но­вых теорий развития Вселенной, физики элементарных частиц, с опровержениями теории относительности и квантовой механики. Я спросил у моего друга, попада­лось ли ему среди этих писем хотя бы одно, содержащее какую-нибудь действительно интересную мысль, заслу­живающую внимания. Ответ был получен мгновенно: «Нет, ни разу мы не получали ничего стоящего». Лично мне глубоко импонируют авторы таких писем, по-моему, люди, размышляющие о судьбах Вселенной, заслужива­ют всяческого уважения. Однако столь же глубоко я убежден, что время дилетантов в большой науке безвоз­вратно прошло.

Научно-популярная литература при всей ее необхо­димости и больших достоинствах имеет один недостаток. Закономерное стремление авторов популярных книг до­ходчиво и просто объяснить довольно сложные проблемы современной науки подчас порождает у читателей иллю­зию полного понимания данного вопроса и толкает неко­торых к конструированию легковесных, доморощенных теорий. Именно для того, чтобы как-то нейтрализовать это вредное побочное влияние, я думаю, будет уместно еще раз напомнить, что Дирак обладал высокими профес­сиональными навыками и как физик, и как математик.

Мы уже упоминали о выдающихся математических способностях Дирака, о той серьезной математической подготовке, которую он получил к моменту приезда в Кембридж. Вообще говоря, математическое начало в творчестве Дирака проявляется очень сильно.

В 1926 году Дирак полгода провел в Копенгагене, в институте Нильса Бора, а затем полгода работал в Гет тингене. Гамов рассказывает, что в то время среди физи­ков и математиков Геттингена была очень популярна такая задачка: как записать все числа от 1 до 100, исполь­зуя только цифру 2 и все возможные алгебраические дей­ствия. Причем двойку можио было употреблять только четыре раза.

Например: 1=2х2/2х2, 2 =2/2+2/2, 5=2²+2/2 и т. д.

Когда Дирака познакомили с условием этой задачи, он очень быстро нашел общее решение, то есть показал, как можно записать любое число N, причем используя цифру 2 только три раза. Вот это решение:

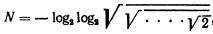  где число корней равно N. Читатель, еще не позабывший школьного курса алгебры, может проверить вывод Дира­ка и оценить элегантность его математического мы­шления.

 

Однако профессионализм сам по себе — это всего лишь гарантия того, что ваши работы будут сделаны на надлежащем уровне. Это гарантия одобрения коллег. Ра­боты же Дирака вызывали не просто одобрение («Хоро­шая, интересная статья!»), они изумляли и восхищали физиков. Идеи, которые он выдвигал, отличались смело­стью, оригинальностью, большой глубиной мысли. Мы упоминали, что уже в своих ранних работах Дирак пора­жал способностью найти новый подход к достаточно ста­рым, вроде бы вдоль и поперек изученным проблемам. Мне кажется, что такая черта характера — умение взгля­нуть на обычное и примелькавшееся свежим взглядом, обнаружить в нем нечто оригинальное, новое — свойст­венна всем выдающимся людям как в науке, так и в ис­кусстве. Корни этой способности следует искать прежде всего в умении удивляться простым и обычным явлени­ям окружающего мира.

У Дирака же эта способность удивляться, смотреть на вещи открытыми глазами, преодолевать инерцию мы­шления была выражена очень ярко. Многие друзья Ди­рака отмечали его умение нестандартно реагировать в самых прозаических ситуациях, Г. Гамов рассказывает, как однажды в Кембридже, в доме Капицы, Дирак об­суждал с Петром Леонидовичем некоторые научные про­блемы. Вместе с ними в комнате сидела жена Капицы и что-то вязала. Окончив обсуждение, Дирак попрощался, однако через некоторое время вернулся, довольно взвол­нованный, и стал объяснять жене Капицы, что по дороге домой он задумался над топологической стороной вяза­ния и ему пришло в голову, что можно вязать и по-дру­гому. Он стал на пальцах показывать изобретенный им новый способ, и оказалось, что Дирак самостоятельно придумал не что иное, как известный всем вяжущим жен­щинам способ, который по общепринятой терминологии называется вязанием «с накидом».

Мало кто знает, что Дирак — этот создатель рафини­рованных физических теорий, обладавший незаурядными математическими способностями, по всем внешним па­раметрам выглядевший как чистый теоретик,— сам ста­вил некоторые эксперименты. Все та же самостоятель­ность мышления позволила Дираку преодолеть клановые предрассудки теоретиков по отношению к «возне с же­лезками». Стремление постичь природу физического яв­ления было для него самым главным, а то, что для этого придется сменить авторучку на гаечный ключ, его не останавливало.

Свою экспериментальную деятельность Дирак вел сов­местно с П. Л. Капицей. Они придумали новый метод разделения изотопов. Суть метода заключалась в том, что поток газа, состоящего из смеси изотопов, заставляли огибать стенку, при этом за счет центробежной силы мо­лекулы газа с разными массами летели по разным траек­ториям. Поэтому в одном месте собирались молекулы более легкого изотопа, а в другом — более тяжелого. Ди­рак сам занимался налаживанием установки для этого эксперимента (между прочим, к тому времени он уже был нобелевским лауреатом). Однако вскоре Капица уехал в Советский Союз, а затем Э. Резерфорд передал в нашу страну все оборудование Мондовской лаборато­рии, и Дирак не смог закончить этот опыт. Интересно, что во время войны группа исследователей в Оксфорде, ра­ботавшая над атомной программой, исследовала возмо­жности такого способа для разделения изотопов урана. Оказалось, что сам метод работает превосходно, но он не так эффективен, как другие способы. Поэтому широкого применения методика Дирака—Капицы не получила.

Почему-то считается, что новатор в на­уке обязательно должен быть холериком с горящими глазами, взлохмаченной шевелюрой и порывистыми дви­жениями. Долгие раздумья сменяются у него моментами творческого озарения, тогда он начинает бегать по «окружающему ландшафту», хватать прохожих за пуго­вицу и излагать им свои замечательные идеи.

Дирак, конечно, абсолютно не напоминал таких ка­рикатурных гениев. Смелость мышления сочеталась у не­го с исключительной аккуратностью и даже педантизмом. Он был скрупулезно точен, последователен и абсолютно не переносил нечетких утверждений ни в своих научных трудах, ни в обычных разговорах.

Карл фон Вейцзекер вспоминает, как однажды вече­ром в компании молодых физиков произошел такой слу­чай. Подали чай, и Вольфганг Паули взял себе слишком много сахара. Это сразу же стало предме­том обсуждения, и кто-то спросил мнение Дирака. Он сказал — после некоторого размышления (!), отмечает Вейцзекер: «Я думаю, что Паули будет достаточно и од­ного куска». Конечно, обсуждение «сахарной проблемы» скоро прекратилось, и разговор пошел своим чередом. Но тут Дирак вдруг заявил: «Я думаю, одного куска сахара будет достаточно любому». Молодые люди, наверное, пе­реглянулись и продолжали разговаривать дальше. А Ди­рак спустя некоторое время еще раз уточнил: «Я думаю, что одного куска сахара, именно таких размеров, будет достаточно любому!»

Другую историю приводит Г. Гамов. Однажды после лекции Дирак отвечал на вопросы слушателей. Кто-то спросил его: «Профессор Дирак, я не понимаю, как вы вывели формулу, которая написана в левом верхнем уг­лу доски».— «Это не вопрос,— сказал Дирак.— Это утверждение. Следующий вопрос, пожалуйста?»

Гамов пишет также, что как-то П. Капица дал почи­тать Дираку «Преступление и наказание» Достоевского. Когда Дирак возвращал книжку, он сказал: «Хорошая книга, но в одной главе автор сделал ошибку. У него солнце в один и тот же день восходит два раза».

Для понимания творческого метода Дирака и его сти­ля работы очень важна следующая цитата: «Мне удалось развить общую теорию преобразований, и это достави­ло мне большое удовлетворение. Я считаю, что из всех работ, которые я сделал за всю свою жизнь, именно эта работа принесла мне наибольшее удовлетворение. Она нравилась мне потому, что не явилась результатом некое­го случайного счастливого стечения обстоятельств, она вытекает из логического обдумывания шаг за шагом, когда видишь, что каждый шаг приводит ко все более детальному знанию и наталкивает на новые вопросы, ко­торые надо исследовать и разрешать. Именно по этому пути, продвигаясь шаг за шагом, я смог прийти к общей теории».

Чем характерно высказывание Дирака? Когда чита­ешь все эти повторяющиеся «шаг за шагом», невольно возникает образ путника, медленно бредущего по пустын­ной дороге. Правда, такое сравнение не совсем точно схватывает весьма существенный момент: Дирак говорит о труде ученого, и «шаг за шагом» приходится идти не по протоптанной аллее парка, а по нехоженым «тропам незнаемого».

Вернер Гейзенберг говорил о Дираке, что «...в своих научных исследованиях он похож на некоторых альпини­стов, взбирающихся на сложную гору. Все дело в том, считают они, чтобы пройти следующие три ярда. Если де­лать это достаточно долго, вы доберетесь до вершины. Пытаться же представить себе все восхождение в целом, со всеми многочисленными трудностями, значит только прийти к разочарованию и потерять уверенность. Ведь и в самом деле, вы сталкиваетесь с настоящими пробле­мами, лишь когда достигаете самых трудных участков скалы». В этих словах мы опять-таки видим подчеркива­ние последовательности, методичности, постепенного про­движения вперед, как характерных особенностей науч­ного стиля Дирака. Однако в науке открытие фундамен­тально новых вещей (а именно этим и славен Дирак) означает преодоление логических тупиков. Двигаясь шаг за шагом, можно лишь благополучно зайти в такой тупик, преодоление его всегда есть некий скачок. Поэтому, поль­зуясь терминологией Гейзенберга, можно сказать, что Ди­рак очень хорошо умел перепрыгивать через трещины.

Кроме того, возвращаясь к высказыванию Дирака, мне хотелось бы обратить внимание читателя на ту часть цитаты, где говорится, что «каждый шаг... наталкивает на новые вопросы, которые надо исследовать и разре­шать». Это тоже очень важная черта Дирака — стрем­ление идти до конца в своих выводах, не бояться возни­кающих трудностей, не сглаживать или вообще оставлять в стороне неизбежно возникающие новые «острые» мо­менты.

Собственно говоря, первая теория антивещества вначале и представляла такую неприятность, которая возникла при успешном завершении одной из самых фундаменталь­ных работ Дирака — релятивистской теории электрона. Огромная заслуга Дирака состоит в том, что он не оста­вил эту побочную неприятность в стороне, а подверг все­стороннему анализу.

 

3. КВАНТОВАЯ  МЕХАНИКА  ПЕРЕД  ОТКРЫТИЕМ  АНТИМИРА

Осенью 1927 года в Брюсселе проходил знаменитый 5-й Сольвеевский конгресс. Эта конференция физиков во­шла в историю из-за легендарной дискуссии, которая раз­горелась между Эйнштейном и Бором по вопросам физи­ческого обоснования квантовой механики. Ситуация, которая сложилась в то время, была достаточно уникаль­ной: при изучении микромира физики столкнулись с кар­динально новыми явлениями, совершенно не имевшими аналогов с тем, что было известно до сих пор.

Судите сами. Классическая физика считала самооче­видным, что любое движущееся тело описывает в про­странстве некоторую траекторию. Причем в каждой точ­ке этой траектории можно измерить одновременно ско­рость тела и его положение в пространстве. Квантовая механика утверждала, что понятие траектории для ми­крочастиц теряет всякий смысл. Если вы точно измерите скорость частицы, то ничего не будете знать о том, где она находится, и наоборот, точно измерив положение частицы, вы ничего не сможете сказать о ее скорости. Но почему?

Классическая физика четко разделяла: есть частицы, отдельные «комочки» вещества, и есть волны, коллективные процессы, в которых участвует много «комочков» ве­щества. Квантовая механика показала, что микрообъек­ты в одних процессах могут вести себя как частицы, а в других явно демонстрируют характерные волновые свой­ства.Но почему?

Классическая физика утверждала: всякая заряжен­ная частица, движущаяся по криволинейной траектории, должна излучать. Из-за этого энергия частицы будет не­прерывно уменьшаться. Оказалось же, что электроны в атоме могут двигаться вокруг ядра сколь угодно долго и не испускать излучения. Никакого непрерывного изме­нения энергии электронов нет, энергия электронов в ато­ме может изменяться только вполне определенными пор­циями. Но почему?

Вся классическая физика покоится на том убеждении, что, зная закон движения частицы и факт появления ее в точке А, мы абсолютно точно можем предсказать, ког­да она попадет в точку В. Квантовая механика утвержда­ет, что, зная закон движения микрочастицы и факт появ­ления ее в точке А, мы можем определить всего лишь вероятность ее появления в точке В. Но как же так?

Все эти вопросы требовали объяснения, все удивитель­ные свойства микрообъектов нуждались в интерпретации. Физики сравнительно быстро нашли основные уравнения квантовой механики и экспериментально показали, что они довольно неплохо описывают действительность. Од­нако понимания того, почему эти законы квантовой меха­ники работают именно так, а не иначе, не было. Процесс установления физического смысла тех величин, которые входят в уравнения квантовой механики, длился долго и протекал, можно сказать, довольно болезненно. Требо­валось пересмотреть самые основные положения физи­ческого мышления, совершить переоценку веками сло­жившихся понятий.

Ситуация, создавшаяся в физике к моменту Сольвеевского конгресса 1927 года, очень напоминала положение дел у средневековых алхимиков. Алхимики в свое время затратили массу труда (полезного и бесполезного). Они получили много интересных результатов, обнаружили большое число неведомых ранее веществ, сконструиро­вали   различные   научные  приборы.   Однако   алхимики могли установить лишь сам факт появления, например, какого-нибудь нового химического соединения. Они мог­ли дать только некоторый рецепт: возьмем определенные вещества в определенных пропорциях и произведем над ними определенные действия — тогда получится искомый продукт.

Так и в физике 20-х годов. С одной стороны, исполь­зовались классические понятия: скорость электрона, его траектория. С другой стороны, имелись чисто квантовые эффекты — волновые свойства электрона, квантование энергии. Понимания того, как соотносятся между собой эти обе стороны действительности, не было, и приходи­лось работать с квантовой теорией, пользуясь чуждым ей языком классических образов. Но это то же самое, что представить циклическую перегонку в виде кормежки пе­ликанов.

О такой неприспособленности нашего повседневного языка для описания явлений микромира очень образно говорил Нильс Бор. Однажды Гейзенберг пригласил его покататься на лыжах в горах. Они жили в заброшенной альпийской хижине, которая соответствовала санитарным стандартам чисто символически. И вот, моя посуду после ужина, Бор сказал: «Наш язык очень напоминает мне это мытье посуды. У нас грязная вода и грязные полотенца, и тем не менее мы хотим сделать тарелки и стаканы чис­тыми. Точно так же и с языком. Мы работаем с неясными понятиями, оперируем логикой, пределы применения ко­торой неизвестны, и при всем при том мы еще хотим вне­сти какую-то ясность в наше понимание природы!»

До 5-го Сольвеевского конгресса 1927 года существо­вало несколько интерпретаций квантовой механики. На­ши сегодняшние представления о природе микромира основаны на том варианте, главным идеологом которого был Нильс Бор. И именно этой трактовке квантовой ме­ханики был дан ожесточенный бой.

Основным противником боровского истолкования был Альберт Эйнштейн. А основным пунктом, против которо­го возражал Эйнштейн, был постулат о вероятностной природе микромира. В классической физике — физике макромира — всегда можно было абсолютно точно пред­сказать какое-нибудь явление, если о нем имелось до­статочно информации. С вероятностями в классической физике тоже сталкивались. Однако это происходило толь­ко в тех случаях, когда просто по техническим причинам нельзя было получить полной информации о рассматри­ваемом процессе.

Согласно же взглядам Бора и его сторонников, для микрочастицы не существует самого понятия «путь», «траектория». Все, что можно узнать о поведении микро­частицы,— это вероятность ее появления в том или ином месте. Причем вероятностная природа микромира имеет совершенно фундаментальный характер. Она возникает отнюдь не из-за того, что мы не очень хорошо знаем свой­ства микрообъектов или не имеем достаточной информа­ции о начальных условиях их движения.

Вероятностный подход к описанию микромира совсем не означает, что само это движение микрочастиц абсо­лютно произвольно и непредсказуемо. Если известны ве­роятности, с которыми осуществляются разные события, то это всегда можно экспериментально проверить. Веро­ятность обнаружить частицу в точке х во время t связана с так называемой волновой функцией частицы Ψ(х, t).

Если мы знаем волновую функцию, то, пользуясь ура­внениями квантовой механики, можем определить веро­ятность появления частицы в любом месте и в любое время. Однако, подчеркиваю, опять-таки только вероятность.

Именно этот момент казался Эйнштейну абсолютно немыслимым, и в течение всей своей жизни он не мог при­мириться с воровской интерпретацией квантовой механи­ки. Эйнштейн настойчиво искал слабые места в системе построений квантовой механики, предлагал различные парадоксы, которые, по его мнению, доказывали несосто­ятельность вероятностного подхода. И, надо сказать, та­кая его активная оппозиция квантовомеханическим идеям сыграла положительную роль. Физики стали лучше понимать смысл вероятностного подхода именно после дискуссий с Эйнштейном. Разрешая парадоксы, предло­женные Эйнштейном, разбирая его критические замеча­ния, Бор и его последователи стали сами лучше понимать сущность своего же учения, обрели четкие формулировки и веские доказательства своей правоты.

Как мы уже упоминали, апогей дискуссий о физиче­ской сути квантовой механики наступил на Сольвеевском конгрессе. Споры Бора с Эйнштейном на конгрессе вошли в историю, сейчас они обстоятельно изучаются всеми ис­ториками и философами естествознания. Несколько дней подряд Эйнштейн каждое утро предлагал Бору очеред­ной мысленный эксперимент, который, по его мнению, не­опровержимо доказывал несостоятельность вероятност­ной трактовки микромира. В течение дня Бор и поддер­живавшие его физики напряженно искали решение, и каждый день к ужину Бор уже был в состоянии показать Эйнштейну, в чем заключалась его ошибка.

Нам для дальнейшего рассказа об истории возникно­вения Антимира очень важно не столько содержание этих легендарных дискуссий, сколько небольшой разговор, ко­торый произошел между Бором и Дираком в перерыве между лекциями. Бор поинтересовался, над чем сейчас работает Дирак, и когда узнал, что тот занят разработ­кой релятивистской теории электрона, то с удивлением заметил: «Но ведь эта проблема уже решена Клейном?» У Дирака не было времени объяснить свою точку зре­ния — началась очередная лекция, и Бор удалился об­думывать очередной парадокс Эйнштейна. Вот и все. Но эта встреча произвела на Дирака глубокое впечатление. Парадоксальность сложившейся ситуации заключалась в том, что задача, при разработке которой было создано знаменитое релятивистское уравнение Дирака, а затем и первая теория Антимира, считалась уже решенной! Считалось, что это уже пройденный этап и думать над ней — лишь напрасная трата времени! Дирак писал, что точку зрения Бора разделяли тогда большинство физи­ков, а возможно, и все.

Рассмотрим теперь все по порядку: что такое реляти­вистское уравнение, в чем состояло решение Клейна и почему Дирак был им недоволен?

4. «НО ВЕДЬ ЭТА ПРОБЛЕМА УЖЕ РЕШЕНА КЛЕЙНОМ?»

Исторически сложилось так, что вначале квантовая механика развивалась независимо от теории относитель­ности. Эффекты, которые рассматривает теория относи­тельности, проявляются только при движении тел с боль­шими скоростями, сравнимыми со скоростью света. Кван­товая же механика изначально строилась как теория явлений, происходящих при малых скоростях. Однако в микромире частицы довольно часто обладают большими скоростями и релятивистские эффекты для них становят­ся уже весьма существеными, если не определяющими. Это было первым основанием для попыток построить ре­лятивистскую квантовую механику. Кроме того, с чисто эстетической точки зрения была необходимость создать теорию, которая бы одновременно удовлетворяла прин­ципам квантовой механики и теории относительности.

Интересно, что человек, который первым нашел реля­тивистское уравнение для квантовой частицы, не осме­лился опубликовать свои результаты. Этим человеком был не кто иной, как Эрвин Шредингер, а не решился он поведать миру о своем релятивистском уравнении пото­му, что оно давало результаты, совершенно не согласую­щиеся с экспериментальными данными. В чем же дело?

Дело в том, что, получив свое релятивистское урав­нение, он решил проверить, как оно работает на примере стандартной задачи расчета спектра уровней атома во­дорода. Эта проблема была хорошо изучена с эксперимен­тальной стороны и казалась наиболее подходящей с те­оретической точки зрения. Действительно, атом водоро­да— простейшая квантовомеханическая система: протон плюс электрон. Но Шредингер тогда еще не знал, что электрон имеет одно важное свойство — спин. Это со­вершенно фундаментальная характеристика каждой эле­ментарной частицы, такая же, как, например, масса или заряд. Наглядно спин можно представить как некоторый вращательный момент, внутренне присущий частице. Правда, наглядность тут довольно сомнительная: вряд ли можно вообразить волчок, вращение которого нельзя ни ускорить, ни замедлить, да к тому же оно не связано ни с каким перемещением в пространстве! На заре кванто­вой механики действительно считали, что электрон вра­щается в буквальном смысле, как веретено. Дирак рас­сказывал, какую злую шутку сыграло это заблуждение с «отцами-основателями» понятия спина С. Гаудсмитом и Д. Уленбеком.

В то время они работали в Лейдене и, написав в 1925 году небольшую работу о спине электрона, показа­ли ее своему профессору П. Эренфесту. Пауль Эренфест сыграл особую роль в развитии квантовой механики. Этот человек обладал исключительно острым критическим умом и незаурядным чувством нового. Гипотеза о спине сразу же понравилась Эренфесту, и он посоветовал Гаудсмиту и Уленбеку рассказать о ней Конраду Лоренцу, большому физику и крупному специалисту в теории элек­трона. В Гарлеме, куда приехали для разговора с Лоренцом Гаудсмит и Уленбек, их ждало сильное разочарова­ние. Лоренц утверждал, что он уже рассматривал такую идею и пришел к выводу, что электрон не может иметь спина, потому что тогда скорость вращения его поверх­ности превышала бы скорость света. Это был убийствен­ный аргумент. Расстроенные Гаудсмит и Уленбек, вер­нувшись в Лейден, попросили Эренфеста отдать назад их работу. Но оказалось уже поздно, Эренфест послал ста­тью в печать. И хотя Лоренц был совершенно прав — в классическом смысле вращение электрона противоре­чит основному постулату теории относительности,— тем не менее спин у электрона существует. Это есть чисто квантовый эффект, не связанный с каким-либо переме­щением поверхности электрона в пространстве.

Как мы говорили, спиновое вращение частицы нельзя ускорить или замедлить. Можно изменить его направле­ние. Однако и направление спина изменяется далеко не произвольным образом. Например, электрон имеет спин 1/2. Это означает, что проекция его спина на любую вы­бранную ось в пространстве может принимать только два значения: «по» и «против» или «вверх» и «вниз». Все промежуточные значения для проекций спина элект­рона запрещены. С математической точки зрения такие свойства спина электрона приводят к тому, что он описы­вается более сложным образом, нежели привычные нам величины. К то­му же проекции спина на оси координат х, у и z не явля­ются просто числами, как для обычных векторов, а мат­рицами. В случае спина 1/2 их называют матрицами Пау­ли.

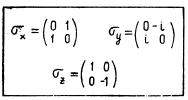 - Матрицы Паули.

 

Стало быть, для того чтобы полностью охарактеризо­вать движение электрона, мы должны знать не одну, а две волновые функции, которые соответствуют вероятно­сти обнаружить электрон в некоторой точке х со спином «вверх» ψ_↑(х, t) и со спином «вниз» ψ_↓(x, t).

Когда Шредингер выполнял свои расчеты с релятиви­стским уравнением, всего этого он еще не знал и спино­вые эффекты, естественно, не учитывал. Именно это об­стоятельство   не   позволило   ему   получить   согласие   с экспериментальными данными. Шредингер не был так смел, как Эренфест, и удачлив, как Гаудсмит и Уленбек. Он не стал публиковать работу о красивом релятивист­ском уравнении, дающем неправильные результаты. Вместо этого Шредингер проанализировал нерелятивист­ский случай и получил свое знаменитое (нерелятивист­ское) уравнение, которое вошло во все учебники кванто­вой механики.

Однако и релятивистское уравнение Шредингера то­же теперь находится в учебниках, правда, под именем открывших его заново в 1926 году О. Клейна и В. Гордо­на (независимо от них в том же году его получил наш из­вестный физик В. А. Фок). Клейна и Гордона не смути­ло расхождение с опытом. Оказалось, что если релятиви­стское уравнение Шредингера применить к некоторым другим проблемам, то получаются вполне разумные ре­зультаты.

Итак, казалось бы, чего желать лучшего. У вас есть квантовое уравнение, удовлетворяющее релятивистским принципам, оно хорошо объясняет некоторый круг задач, и его решения согласуются с основными физическими законами. Правда, оказалось, что если вычислить соглас­но уравнению Клейна—Гордона вероятность обнаруже­ния электрона в том или ином месте, то получалось, что она в принципе могла быть и отрицательной. С точки зрения здравого смысла отрицательная вероятность — такой же нонсенс, как квадратный круг. Но в те замеча­тельные годы в квантовой механике появилось много идей, гораздо более «диких», чем отрицательная вероят­ность, и тем не менее прекрасно работающих. Поэтому совсем не удивительно, что научная общественность в це­лом была вполне удовлетворена уравнением Клейна— Гордона. Даже Бор, как мы помним, удивился, когда узнал о том, что Дирак занимается релятивистской тео­рией электрона: «Но ведь эта проблема уже решена Клей­ном?»

Однако Дирак имел собственное мнение и никак не мог разделить общее благодушие, царившее вокруг этого вопроса. Причина заключалась в том, что отрицательные вероятности никаким образом не могли быть совмещены с любимой теорией Дирака — теорией преобразований.

Как мы знаем, волновая функция ψ(х, t) позволяет определить вероятность той или иной координаты частицы в определенный момент времени. А какова вероятность обнаружить у частицы наперед заданный импульс, энер­гию или угловой момент? Ответ на это и давала теория преобразований. Дирак показал, как, зная координатную волновую функцию ψ(х, t) можно найти вероятность то­го, что произвольная динамическая переменная (будь то импульс или энергия) приобретет заданное значение. По сути дела, эта работа Дирака привела квантовую меха­нику к логическому завершению: теперь, зная ψ(х, t), вы могли определить все характеристики частицы. Однако если у электрона вероятность обрести какое-либо значе­ние координаты становилась отрицательной, теорию пре­образований применять было невозможно. С этим Дирак никак не мог смириться. «Теория преобразований стала моим любимым детищем (my darling), и меня не интере­совала ни одна из теорий, которые не подходили для моего любимого творения»,— говорил в своих воспомина­ниях Дирак.

Надо подчеркнуть большое научное мужество Дира­ка. Ведь одно дело общие слова о том, что теория долж­на быть красивой и внутренне согласованной, а другое — когда вы начинаете вести конкретные исследования, которые большинство физиков считают полностью ли­шенными смысла.

Однако Дирак глубоко верил, что красивая математи­ческая теория не может быть неверной! В своих выступ­лениях он постоянно подчеркивает эту мысль. Подобно средневековому рыцарю, который повсюду сражался во имя красоты своей дамы, Дирак все время отстаивал принцип красоты физической теории как главный крите­рий ее истинности. В статье, посвященной столетию со дня рождения Эйнштейна, он ставит вопрос прямо: что произошло, если бы вдруг был сделан эксперимент, про­тиворечащий такой красивой и логически замкнутой тео­рии, как общая теория относительности? Следовало бы тогда объявить теорию в корне неверной? Дирак пишет: «Я сказал бы, что ответом на этот вопрос должно быть решительное нет. Любой, кто понимает глубокую гармо­нию, связывающую между собой явления природы и об­щие математические принципы, должен чувствовать, что если теория так прекрасна и изящна, как теория Эйн­штейна, то она в основном безусловно верна. Если в ка­ком-то случае применения такой теории появляется рас­хождение с наблюдениями, то его причиной, видимо, яв­ляются второстепенные факторы, которые относятся к этому применению и которые не были должным образом учтены, но никак не неправильность общих принципов теории».

 

5. УРАВНЕНИЕ  ДИРАКА

Серьезный разговор об уравнении Дирака — это зада­ча не для научно-популярной книжки. Однако мне очень хотелось, чтобы читатель получил некоторое представле­ние о том, каким был ход рассуждений Дирака.

Дирак вспоминал, что начал работать над своей реля­тивистской теорией, «играясь с уравнениями, а не пыта­ясь ввести какую-нибудь определенную физическую идею». В чем же состояла эта игра Дирака?

Он хотел найти такое уравнение, которое, во-первых, было бы релятивистским, то есть удовлетворяло принци­пам теории относительности, во-вторых, подчинялось бы требованиям его любимой теории преобразований и, на­конец, в-третьих, было бы квантовомеханическим урав­нением, описывающим движение электрона.

Но что значит «релятивистское уравнение»? Одним из характерных признаков такого уравнения является то, что в него должны входить совершенно равноправным образом как пространственные координаты х, у, z так и временная координата t. Далее, уравнение должно быть квантовомеханическим, то есть содержать волновую фун­кцию электрона ψ(x, у, z, t).

Гораздо труднее дело обстояло с непременным жела­нием Дирака, чтобы будущее уравнение подчинялось тео­рии преобразований. Однако было известно, что, сделав соответствующие квантовомеханические трансформации, уравнение Клейна—Гордона можно получить непосред­ственно из знаменитого соотношения теории относитель­ности Е=mс². Надо заметить только, что это уравнение связывает энергию и массу покоящегося тела. Если же тело движется со скоростью v, то  есть  имеет  импульс p=mv, то соответствующее релятивистское уравнение бу­дет:

Е²= p²+ m²                                                                (1)

(для удобства мы работаем в системе единиц, где ско­рость света с=1). Именно из уравнения (1) можно вывести уравнение Клейна—Гордона, но оно, как мы зна­ем, приводит к отрицательным вероятностям.

С математической точки зрения все эти неприятности происходят из-за того, что уравнение Клейна—Гордона содержит квадрат энергии — Е². Вот если бы найти ре­лятивистское уравнение, в которое энергия Е входила бы в первой степени... Тогда бы можно было удовлетво­рить требования теории преобразований и избежать от­рицательных вероятностей. Но в чем проблема? Давайте извлечем квадратный корень из левой и правой части уравнения (1), и получим Е в первой степени

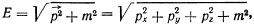                        (2)

 здесь р_х, р_у, р₂— проекции импульса р на оси координат.

Всем хорошо уравнение (2), кроме одного: в нем на­рушена нужная нам «демократия» между пространствен­ными и временной координатами. Дело в том, что в кван­товой механике проекции импульса p_х, p_у, p_z связаны с пространственными координатами х, у, z, а энергия Е — с временной координатой. Видно, что в уравнение (2) энергия Е входит в первой степени, а проекции импульса p_х, p_у, p_z — во второй. Следовательно, здесь нет равно­правия между координатами х, y, z и t. Для восстановления «справедливости» надо найти та­кое выражение X, куда бы проекции p_х, p_у, p_z входили в первой степени. Кроме того, должно выполняться ра­венство Е=Х,             (3)

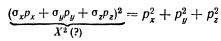
 Видно, что это выражение очень похоже на уравнение (4), но только оно содержит сумму трех квадратов, а нам нужно получить сумму четырех квадратов. Тем не менее Дирак почувствовал, что находится на правильном пути и надо искать именно в этом направлении, то есть попы­таться сконструировать подходящее выражение, исполь­зуя матрицы Паули.

Если вы вернетесь к рисунку, на котором изображены матрицы Паули, то увидите, что это матрицы два на два, то есть у них 2 столбца и 2 строки. Дирак же решил скон­струировать из них матрицы большей размерности, состо­ящие из 4 столбцов и 4 строк. Оказалось, что с помощью таких матриц легко получается выражение для квадрат­ного корня из суммы четырех квадратов: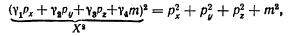 

где γ_i — некоторые матрицы 4X4, построенные из матриц Паули.

 

 

Вот так было открыто одно из самых основных урав­нений современной физики. Как потом говорил Дирак: «На нем стоит большая часть физики и вся химия».

 

 

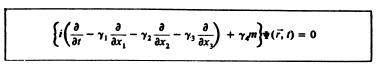
Заметим, что в уравнение Дирака вошли матрицы Па­ули, но, как мы говорили раньше, они связаны со спином 1/2. Поэтому не удивительно, что решения уравнения Дирака описывают движение частицы со спином 1/2. Удиви­тельно другое: в намерение Дирака не входило создание теории частиц со спином. Как мы видели, он хотел просто привести в соответствие релятивистские принципы и тре­бования его любимой теории преобразований. И этот синтез вдруг дал неожиданные плоды. Оказалось, что су­ществование фундаментальной характеристики частицы — спина — естественным образом возникает при объе­динении квантовой механики и теории относительности. Это был подлинный триумф теории Дирака!

На современников открытие Дирака произвело потря­сающее впечатление. И в большей мере из-за того, что путь, по которому пошел Дирак, был совершенно неожи­данным. Выдающийся современный физик Юджин Вигнер вспоминает, что именно в то время, совместно с дру­гим большим физиком Паскуалем Иорданом, они тоже пытались построить релятивистское уравнение для час­тиц со спином 1/2. Как мы уже говорили, такие частицы имеют только два состояния (спин вверх—спин вниз), по­этому вполне естественно было полагать, что искомое уравнение будет тоже двухкомпонентным. Совершенно случайно они узнали о работе Дирака: Макс Борн попро­сил его написать отзыв о работе одного автора. Дирак прислал письмо с советами, как сделать статью более «читаемой», и в конце письма в десяти строчках упомя­нул о своей работе по теории электрона и выписал свое четырехкомпонентное уравнение. «Мы с Йорданом были просто ошарашены (were quite flabbergasted)»,—пишет Вигнер. В конце концов Йордан сказал: «Да, конечно, хорошо было бы, если бы мы нашли это уравнение. Но вывод его так красив, а само оно содержит столько смыс­ла, что мы вообще должны быть счастливы, что оно су­ществует».

А теперь, дорогой читатель, попробуйте поставить се­бя на место Дирака и угадайте, как он реагировал на свое открытие? Воскликнул «Эврика!», побежал за шам­панским или просто лег спать? Ни за что не угадаете!

Известный английский писатель Чарлз Сноу вспоми­нает, как Дирак однажды признался ему, что он почувст­вовал, когда вывел свое знаменитое уравнение. Прежде всего Дирак сразу прикинул, описывает ли оно спектр энергий атома водорода. Оказалось, все в порядке. «И тут,— говорит Дирак,— я так страшно испугался, что не мог пошевельнуться!» Но почему? Дирак объясняет Сноу, что, занимаясь творческой работой, человек всегда испытывает большие сомнения и большие надежды. При­чем всегда наибольшие опасения охватывают исследова­теля именно в тот момент, когда он должен сделать ре­шающий шаг вперед. В качестве примера Дирак говорит о К. Лоренце, который имел в своих руках все, чтобы создать специальную теорию относительности, но так и не отважился сделать решающий шаг.

Итак, оказалось, что квантовое уравнение, записан­ное с учетом требований теории относительности, есте­ственным образом описывает поведение частиц со спи­ном. Это было для физиков приятным сюрпризом. Но релятивистское начало в квантовой теории порождало целый ряд новых проблем. Как признавался Дирак, осмысление физических выводов, которые следуют из его уравнения, заняло у него гораздо больше времени и сил, чем вывод самого уравнения. Эти исследования «неприят­ных» следствий, возникающих при решении релятивист­ского квантового уравнения для электрона, и привели к созданию первой теории Антимира — теории дырок.

 

6. ОТРИЦАТЕЛЬНЫЕ  ЭНЕРГИИ,  «ОСЛИНЫЕ ЭЛЕКТРОНЫ», ТЕОРИЯ   ДЫРОК И   ПУЗЫРЕК  С ЛЕКАРСТВАМИ

Осень чувствовалась везде. И в голых ветках деревь­ев, и в шуршании листьев под ногами, но главное — воз­дух становился особенно прозрачным и холодноватым. Хорошо думалось. Двое вышли из лесной аллеи и не спе­ша стали подниматься по невысокому холму. Они шли молча, погруженные в свои мысли. Однако тишину все время нарушало какое-то слабенькое, но достаточно про­тивное треньканье.

— Извините, профессор,— сказал более молодой из мужчин.— Я немного простыл и вынужден носить с со­бой склянку с аспирином.

Профессор, тоже достаточно молодой человек, лет 30, немного помолчал. Затем серьезно заметил: «Полагаю, шум от вашего пузырька будет максимальным, когда он заполнен таблетками наполовину. Не так ли?»

Английский физик Рудольф Пайерлс, рассказавший эту маленькую историю об одной прогулке Поля Дирака и его ассистента, замечает: «Мне стало ужасно интерес­но, произошел ли этот случай до или после изобретения Дираком теории «дырок». Я навел справки, и оказалось, что это было в середине 30-х годов, теория «дырок» уже была создана, и замечание Дирака становится понятным».

В этой главе мы постараемся объяснить читателю, в чем же заключается аналогия между дребезжащим пу­зырьком с таблетками и теорией дырок.

Уже в своей классической работе по релятивистской теории электрона Дирак отмечал существование двух трудностей. Первая трудность состояла в том, что кван­товая механика того времени не могла правильным обра­зом учесть эффекты спина электрона. Вторая трудность возникала из-за того, что в релятивистском подходе элек­трон получал возможность иметь отрицательную энергию. В предыдущей главе мы видели, как блестяще справился Дирак с решением первой проблемы. Однако проблема отрицательных энергий не давала покоя Дираку еще в течение нескольких лет.

Понять, как возникают отрицательные энергии и к каким неприятным последствиям это приводит, можно на примере хорошо знакомого нам релятивистского соот­ношения, связывающего энергию частицы E с ее массой m и импульсом р (для последующего изложения нам не важно, что импульс частицы — это вектор, и мы будем опускать стрелку над буквой р)

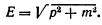
Еще со школьной скамьи мы знаем, что перед квад­ратным корнем можно поставить либо знак плюс, либо минус. То есть                 

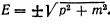                                              (1)

Следовательно, релятивизм не запрещает частице иметь отрицательную энергию. Однако в неквантовой тео­рии (то есть в классической физике или в релятивистской теории) энергия частицы меняется непрерывно, начиная с некоторого минимального значения. Как нетрудно видеть, минимальной энергией обладает покоящаяся час­тица, то есть у которой p=0. Тогда E_min = ±m.

На рис.  видно, что область E>0 отделена от облас­ти E<0 промежутком в 2m и частица с положительной энергией никогда не сможет попасть в область отрица­тельных Е, если ее энергия меняется непрерывно. В кван­товой теории энергия частицы меняется скачком, и у нее в принципе есть возможность «перепрыгнуть» из области E>0 в область E<0. Поэтому при решении уравнения Дирака возникают две полностью равноправные с мате­матической точки зрения возможности: либо частица дви­жется как обычно, с положительной энергией, либо с отрицательной. А что такое движение частицы с отри­цательной энергией?

Представить это себе довольно трудно, в обычной, повседневной жизни все тела движутся только с положи­тельной полной энергией. Правда, когда мы сталкиваемся с квантовыми явлениями, наше воображение отказы­вает во многих случаях. Поэтому то, что мы не в состоя­нии представить частицу с отрицательной энергией, само по себе не является каким-то криминалом. Однако стро­гое математическое рассмотрение показывает, что элект­рон с отрицательной энергией (Е<0) должен двигаться во внешнем поле как частица с положительным зарядом. Тогда при переходе электрона из области с E>0 в об­ласть £<0 знак его заряда должен измениться на проти­воположный. Это противоречит закону сохранения элек­трического заряда. Таким образом, состояния с отрица­тельной энергией страшны не столько сами по себе, сколько тем, что переходы в эти состояния нарушают законы сохранения. Вот если бы как-то удалось запретить электрону совершать скачки из области положительных энергий!..

Это означает, что если энергия Е положительна, то масса m должна быть отрицательной! Представить себе в нашем мире частицу с отрицательной массой еще труд­нее, чем с отрицательной энергией.

Сила, приложенная к телу, будет вызывать его движе­ние в противоположном направлении! Если бы мы захо­тели сыграть в футбол с мячом отрицательной массы, то, чтобы забить его в чужие ворота, надо было бы бить мяч в направлении своих ворот. Если бы вы попытались оста­новить мяч отрицательной массы, то он полетел бы еще быстрее, и наоборот, при ударе с лета такой мяч прилип бы к ноге. Вообще говоря, нам вряд ли удалось бы поза­бавиться антифутболом. Мяч отрицательной массы в по­ле тяжести Земли просто взял бы и воспарил вверх. Теперь, я думаю, понятно, почему Г. Гамов метко при­своил электронам с отрицательной массой прозвище «ослиные электроны».

Как же все-таки ликвидировать трудности с отрица­тельными энергиями и отрицательными массами? Не до­пускать же в храм науки «ослиные частицы».

И вот здесь Дирак опять предлагает совершенно не­ожиданное решение. Одним из основных свойств частиц с полуцелым спином является то, что никогда любые две из них не могут находиться в одном и том же состоянии. Если у таких частиц одинаковые энергии, то проекции спина должны быть разными или, наоборот, если проек­ции спина одинаковы, то энергии частиц должны отличаться. Это фундаментальное свойство частиц с полуце­лым спином называется принципом Паули.

Так вот, Дирак смело предположил, что в нашем мире все состояния с отрицательной энергией полностью заня­ты электронами. Поэтому в силу принципа Паули элек­трон из области положительных энергий никогда не смо­жет перепрыгнуть в область отрицательных энергий. В этом смысле электрон с положительной энергией похож на командировочного, который безнадежно томится в холле переполненной гостиницы —все номера заняты.

Итак, проблема с отрицательными энергиями решает­ся следующим образом. Само существование состояний с отрицательной энергией, по Дираку, разрешается, пе­реходы в эти состояния запрещены. Однако какой ценой достается это решение! Для того что­бы электрон совершенно никуда не мог деться из области положительных энергий, число заполненных состояний с отрицательной энергией должно быть бесконечно! Это означает, что вакуум должен обладать бесконечным от­рицательным зарядом, бесконечной отрицательной энер­гией и бесконечной плотностью. Тем не менее Дирак утверждает, что такой «дикий» вакуум не испортит ника­кие физические характеристики любой системы. Его ар­гументы таковы: все, что мы может наблюдать, это откло­нения, допустим, заряда или энергии системы от заряда или энергии вакуума. Но само отклонение всегда остается неизменным, оно не зависит от того, каков заряд или энергия вакуума.

Если удивительная ситуация, предложенная Дираком, и в самом деле осуществляется, то иными должны быть все наши представления о вакууме. Раньше это было пустое пространство, место без вещества, теперь же, ока­зывается, оно битком набито электронами. Именно пото­му вакуум пуст, в нем ничего не происходит. Подобно пузырьку, туго заполненному таблетками, вакуум «не дребезжит»! (Вы вспоминаете рассказ Р. Пайерлса, ко­торый мы привели в начале главы? Теперь его суть дол­жна быть вам ясна.)

Однако все-таки существует процесс, который позво­лит нам судить, так ли уж вакуум совершенно пуст или «внутри» него что-нибудь да есть.

Возьмем для этого гамма-квант большой энергии E, достаточной, чтобы преодолеть энергетическую щель ши­риной 2m и вытащить электрон из вакуума (то есть Е_у ≥ 2m). Тогда в области положительных энергий появится электрон, а в отрицательной области образуется дырка. Но каков физический смысл этой дырки? Рас­смотрим подробно процесс ее появления.

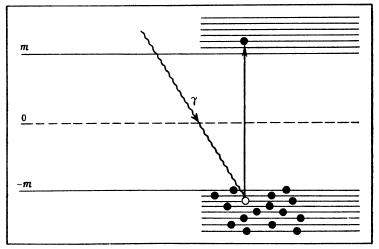
1. Исходное положение — никаких частиц нет: заряд 0, масса 0.

2. Появился гамма-квант и выбил электрон: заряд —е, масса +m.

3. Посчитаем электрические заряды: гамма-квант   заряд 0,  электрон    заряд   —е, дырка        заряд   +е.

4. Посчитаем баланс энергий: был гамма-квант  Е_у ≥ 2m, стал электрон  Е_е- = m, осталось для дырки   Е_д  ≥ m.

5. Следовательно, у дырки заряд +е, масса ≥ m.

Таким образом, если вакуум «не пуст», то γ-кванты могут выбивать из него электроны и частицы с положительным зарядом и положительной массой. Однако если величина положительного заряда предсказывается для Дырки совершенно однозначно — она равна заряду элек­трона, взятому с положительным знаком,— то масса дыр­ки точно не определена. Видно только, что ее масса дол­жна быть больше или равной массе электрона.

Подведем итог: теория электрона Дирака имеет труд­ности — наличие отрицательных энергий. Чтобы их избе­жать, заполним все состояния с отрицательной энергией электронами. Но если вы попытаетесь «вытащить» такой электрон из вакуума, то происходит некоторый фокус — в конечном состоянии появляется не одна частица, а две: обычный электрон и еще некоторая частица с зарядом + е и положительной массой (дырка). Что это за части­ца?

Тут надо сделать некоторое отступление.

У меня на столе лежит справочник элементарных час­тиц, датированный апрелем 1980 года. В нем я насчитал около 170 элементарных частиц. Если еще учесть антича­стицы, то эту цифру надо увеличить раза в два. Ясно, что открытие еще одной или нескольких элементарных час­тиц теперь никого не удивляет, разве что они вдруг ока­жутся с какими-нибудь совсем экзотическими свойства­ми. Сейчас любой пик на экспериментальной кривой с легкостью объясняют существованием новой частицы.

Совершенно другой психологический климат был во времена накануне открытия позитрона. Электрон, протон и фотон — вот все элементарные частицы, известные тог­да физикам. Собственно говоря, большего они и не жела­ли. Есть квант света — фотон, квант отрицательного элек­тричества — электрон, а положительного — протон. Что еще нужно? Физики были внутренне не подготовлены к тому, что элементарных частиц окажется так много. По­этому совсем не удивительно, что Дирак сообразно с царившими тогда настроениями не стал отождествлять дыр­ку с какой-то новой частицей, а сначала решил, что дыр­ки — это обычные протоны. Такое предположение имело несколько привлекательных моментов. Во-первых, если оно оказывалось справедливым, то теория Дирака стано­вилась применимой не только к электронам, но и к про­тонам! То есть вы получали всеобъемлющую теорию как отрицательного, так и положительного электричества. Во-вторых, чисто психологический момент: не нужно было вводить ничего лишнего.

Но напомним, что дырка—это незаполненное элект­ронное состояние. И каким образом это электронное со­стояние приобретает массу протона, который почти в 2000 раз тяжелее электрона, было не ясно.

Кроме того, главная трудность, которую такая трак­товка дырок не могла преодолеть, состояла в следующем.