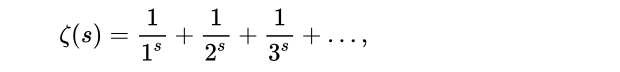89-летний британский математик, сэр Майкл Фрэнсис Атья (Michael Francis Atiyah), лауреат премий Абеля и Филдса, известный своим вкладом в алгебраическую геометрию и топологию, заявил об успешном доказательстве гипотезы Римана. Это знаменитое утверждение описывает то, как расположены на числовой прямой простые числа. Математик представит «простое доказательство, использующее кардинально новый подход» утром в понедельник, 24 сентября. Математическое сообщество скептически относится к заявлению математика.
Гипотеза Римана — одна из семи проблем тысячелетия, наряду с доказанной Григорием Перельманом гипотезой Пуанкаре и теорией Янга-Милса. Она формулируется следующим образом. Возьмем функцию — в каждой точке s она равна сумме ряда:
Этот ряд сходится при s больших единицы. С помощью специальных математических приемов можно расширить эту функцию на всю комплексную плоскость — получится дзета-функция Римана. Причем в некоторых точках комплексной плоскости значения этой функции окажутся равны нулю, например, в отрицательных четных точках. Эти действительные нули называются тривиальными. Но кроме них есть и другие нули, комплексные — например, s = 0,5 ± 21,022040i. Гипотеза Римана утверждает, что все нетривиальные нули дзета-функции лежат на линии Re=0,5 комплексной плоскости.
Риман показал, что зная нетривиальные нули дзета-функции можно построить функцию распределения простых чисел, которая показывает, сколько есть простых чисел, не превышающих данное число. Справедливость гипотезы Римана позволит доказать утверждения и не связанные с простыми числами — например, касающиеся вычислительной сложности различных алгоритмов.
Гипотеза Римана была сформулирована в 1859 году и до сих пор не была доказана или опровергнута. В анонсе своей лекции Майкл Атья указывает, что нашел простое доказательство, «основанное на работах Нейманна (1936), Хирцебруха (1954) и Дирака (1928)». Согласно программе конференции, продолжительность лекции составит всего 45 минут.
Хотя Атья является лауреатом крупнейших математических премий, многие математики с осторожностью отнеслись к заявлению коллеги. Некоторые сравнивают попытку простого доказательства гипотезы Римана с фразой Пьера Ферма, о том, что «остроумное доказательство оказалось слишком длинным, чтобы привести его на полях».
Майкл Атья внес огромный вклад в алгебраическую топологию, заложив основы топологической К-теории. Один из известнейших результатов математика — теорема Атьи—Зингера об индексе, использующаяся при анализе дифференциальных уравнений, к примеру, в теоретической физике.