О ФРАКТАЛЬНОЙ СТРУКТУРЕ ПРОСТРАНСТВА, ВЫЯВЛЯЕМОЙ В ХОДЕ ИССЛЕДОВАНИЙ ЭФФЕКТА МЕСТНОГО ВРЕМЕНИ

 1. Введение

Самое общее содержание феномена макроскопических  флуктуаций, одним из проявлений которого является  эффект местного времени, состоит в неслучайном  характере формы гистограмм,  построенных по коротким,  непересекающимся отрезкам временных рядов флуктуаций в ходе процессов различной  природы. Исследуя подобие формы для пар гистограмм, разделенных различными временными интервалами [1], был обнаружен ряд феноменов, наиболее значительными  среди которых можно назвать  существование различных  периодов – суточного, около 27-суточных, годичных  [2–4], а также  эффект местного времени [5–8].

Эффект местного времени состоит в повышенной вероятности сходства тонкой структуры для пар гистограмм разделенных интервалом равным разности местного времени. Существование этого эффекта было показано для различных расстояний между местами проведения измерений: от, практически,  максимально  возможных  на Земле (ок. 15 тыс. км) до расстояний порядка  одного метра. Также  необходимо отметить, что эффект местного времени наблюдается  для процессов различной  природы [2–4].

Идею организации  эксперимента  по исследованию эффекта местного времени дает рис. 1. Здесь 1 и 2 – источники  флуктуаций, фиксированные  на расстоянии  L друг от друга и движущиеся  с некоторой скоростью V, так,  чтобы линия, соединяющая  источ ники  флуктуаций, была  коллинеарна  вектору  скорости  измерительной  системы.  При этом, через время t₀  равное

t₀ = L/V                                                      (1)

источник  флуктуаций 1 попадет  в то же  место пространства,  где до этого находился источник  2. На  рис.  1 эти  новые положения  показаны  как  1'   и 2'.  Как  оказалось,  и в этом состоит главное содержание  эффекта местного времени, одинаковые  простран- ственные положения обуславливают подобие формы гистограмм, разделенных  интервалом времени t₀, что выражается появлением пика на результирующем  распределении интервалов.

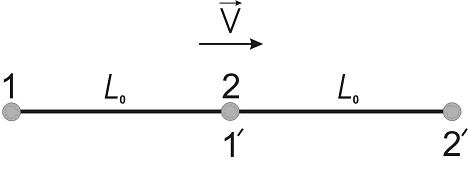
Рис. 1. Иллюстрация возникновения эффекта местного  времени

В предыдущих работах [6–8] было показано, что при увеличении разрешающей способности (уменьшении длительности  используемых гистограмм)  пик местного времени расщепляется  на два субпика. При этом, было найдено, что отношение величины этого расщепления t₁  к величине разности местного времени t₀  равно k = 2.78·10⁻³. Эта величина,  с высокой точностью,  оказалась  равной отношению величины  расщепления суточного периода 240 сек к самому периоду T  = 86400 сек [7, 8]. Это позволило рассматривать  эффект местного времени и суточный период, как феномены одной природы. Поэтому, суточный период рассматривается, как предельный случай эффекта местного времени, когда величина t₀  принимает максимально  возможное значение, обусловленное скоростью вращения Земли вокруг своей оси.

В работе [8] было высказано  предположение,  что субпики, обнаруженные  при расщеплении пика местного времени, также могут расщепляться, при дальнейшем увеличении временного разрешения  метода  исследований.  При этом, последовательность расщеплений t_n  дается выражением:

 t_n  = k_nt₀,      n = 0, 1, 2, ...                                       (2)

Предварительные результаты, полученные в [8] частично  подтвердили  это предположение. В настоящей работе представлены  дальнейшие результаты исследований расщеплений пика местного времени – расщепления второго порядка.

Легко видеть из (2), что исследование каждого  последующего расщепления,  требует повышения разрешающей  способности метода,  более чем на два порядка.  Поэтому, представляется наиболее удобным,  исследовать  расщепления  суточного  периода,  т. к. в этом случае,  значения  t_n , согласно (2), будут иметь максимальную  величину.  Это позволяет  снизить требования  к частотным  свойствам регистрирующей  аппаратуры  и используемым источникам флуктуаций.

  2. Метод исследования и основные результаты

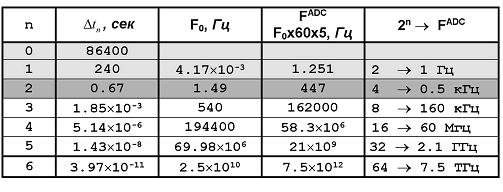
Исходя  из  (2)  можно  рассчитать   величины  t_n.  Результаты такого  расчета  для суточного периода  t₀  = 86400 сек приведены  в Табл.  1. В первом столбце таблицы приведены значения  n, для которых были рассчитаны  величины t_n  (второй столбец), соответствующие t_n частоты вхождения гистограмм в последовательность,  F₀ (третий столбец), частоты сбора данных, обеспечивающие требуемое разрешение при определении t_n   – F ^ADC (четвертый  столбец). При определении F ^ADC  предполагалось,  что гистограммы строятся по 60-точечным отрезкам временных рядов, а искомое расщепление t_n  должно  быть порядка  пяти  гистограмм.  Последний  столбец содержит  суммарное число расщеплений и усредненные частоты сбора данных. Первые две строки таблицы, выделенные  цветом,  относятся  к  суточному  периоду  (первая  строка)  и расщеплению первого порядка  t₁  (вторая  строка),  которые, как отмечалось выше, хорошо изучены. Третья  строка, выделенная более темным цветом, содержит информацию, являющуюся предметом изучения настоящей статьи. Строки 1–5 относятся к расщеплениям, которые могут быть, в принципе, изучены современными средствами эксперимента. Шестая строка, в настоящее время, не может быть исследована. Также  необходимо отметить, что до проведения соответствующих исследований, существование расщеплений порядка выше второго  гипотетично.  Оценки,  приведенные  в четвертом  и пятом  столбцах  таблицы, являются  приблизительными  и служат  для ориентировочного определения параметров, которые должны  быть выдержаны в соответствующих экспериментах.  Реальные  значения этих параметров  могут слегка отличаться  от приведенных в Табл.  1.

 Табл. 1. Результаты расчета  величин расщепления  суточного периода и соответствующих частот,  необходимых для сбора данных

  
 Для  проверки  предположения  о существовании  расщеплений  второго порядка  использовался метод последовательных  уточнений положения уже известных пиков: "солнечного"  – 1440 мин и "звездного"  – 1436 мин. Суть данного метода иллюстрирует  рис.2, где схематично  представлены  хорошо исследованные,  в одноминутном  разрешении, солнечный и звездный пики. Эти пики и прилегающие к ним 30-сек окрестности формируют множество интервалов,  исследуемых при помощи 10-сек гистограмм,  показанных на рис. 2 отдельными  столбиками.  Нулевой  интервал,  выделенный  на рис. 2 черным цветом, соответствует  моменту относительно которого выровнены последовательности гистограмм  – гистограммы  с совпадающими  номерами.  Эти  гистограммы  разделены интервалом времени равным длительности  солнечных суток – 86400 сек. Величины интервалов,  указанные  на рис. 2 даны относительно нулевого интервала,  т. е., за вычетом суточного периода.

После получения распределения интервалов  для 10-сек гистограмм,  положение солнечного и звездного пиков будет известно с точностью ±10 сек. Далее, описанная процедура повторяется,  но с использованием 2-сек гистограмм. После этого, распределение интервалов  для 2-сек гистограмм,  дает возможность  повторить  ту же процедуру с ис- пользованием гистограмм  длительностью  0.2 сек.

Для получения временных рядов, пригодных для применения описанных выше про цедур, были проведены три серии измерений 2, 3 и 4 ноября 2007 г. Каждое  измерение включало  в себя две записи флуктуаций тока обратно смещенного p-n перехода длиной 50000 и 19200000 точек, измеренные с частотой 5 Гц и 8 кГц соответственно. На основе этих временных рядов строились две идентичные последовательности гистограмм.  При этом, гистограммы,  имеющие одинаковые номера были разделены интервалом времени, равным  длительности  солнечных суток – 86400 сек. Пары  гистограмм  с одинаковыми номерами соответствуют нулевому интервалу, показанному на рис. 2, более темным цветом.

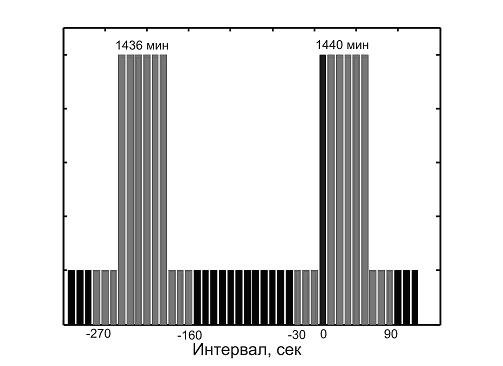
Рис. 2. "Солнечный"  – 1440 мин  и "звездный" – 1436 мин  пики  в расщеплении  суточного периода. Диаграмма иллюстрирует метод последовательных уточнений положения уже известных пиков - серыми столбцами  показаны интервалы,  соответствующие 10-сек гистограммам. Нулевой  интервал  (выделен  черным  цветом)  соответствует моменту относительно которого выровнены последовательности гистограмм  - гистограммам с совпадающими  номерами,  которые разделены интервалом времени  равным длительности солнечных  суток – 86400 сек

Необходимо отметить,  что  длительность  солнечных  суток,  как  правило,  не равна точно 86400 сек, но колеблется  в течение года. Характер  этих колебаний описывается уравнением  времени [9, 10]. Время  для  получения  временных  рядов,  используемых  в настоящей  работе,  было выбрано  так,  чтобы  оно совпадало  с одним из экстремумов уравнения времени: 2–4.11.2007. Это обеспечивает наиболее стабильную продолжительность солнечных суток в течение времени измерений.

Распределения   интервалов,  полученные  в результате  попарного  сравнения  гистограмм  показаны  на  рис.  3. Верхний  рисунок  (рис.  3) содержит  распределение  интервалов,  полученное  с использованием  10-сек гистограмм.  Последовательность  этих гистограмм  строилась  на основе 50000-точечного временного ряда,  измеренного с частотой 5 Гц. Гистограммы  строились на основе 50-точечных отрезков временного ряда. Были  получены две последовательности,  состоящие из 1000 гистограмм,  каждая, кото- рые сравнивались  между  собой для  интервалов  отмеченных  серым цветом на рис. 2. Как  следует  из приведенного  на рис. 3 распределения  интервалов,  в окрестности, показанных  на рис. 2 1-мин пиков снова получены два одиночных пика,  разделенных интервалом равным 240 ± 10 сек.

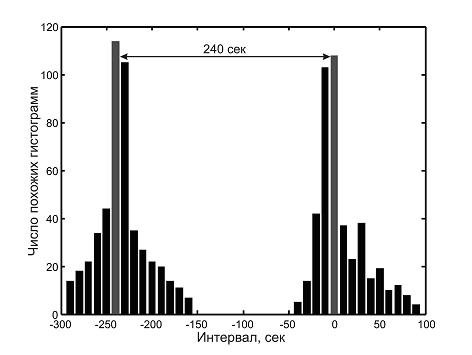
Рис. 3. Распределение  интервалов  для 10-сек гистограмм

  3. Обсуждение

Как  отмечалось  во введении, эффект местного времени исследован  для  широкого диапазона расстояний между местами проведения измерений, вплоть до расстояний порядка одного метра. В последнем случае, время, необходимое, для получения временного ряда  флуктуаций, длина которого будет достаточна  для получения  распределения  интервалов,  составляет  доли секунды. В течение этого времени, внешние (как  правило  – геофизические)  влияния  на измерительные  системы 1 и 2 (рис. 1) с высокой точностью одинаковы.  Учитывая  это, а также  предпринимаемые  меры  по экранированию  1 и 2 от внешних полей, стабилизации источников питания и т. д., единственным изменением, происходящим с системой, является  изменение ее пространственного положения, как это показано  на рис. 1. С этим утверждением  согласуются  также  устойчиво получаемые  в многочисленных экспериментах  результаты, которые всегда находятся  в согласии с (1). Необходимо отметить, что формула  (1) справедлива также для источников флуктуаций, которые находятся  в движении относительно поверхности Земли [11].

Из всего сказанного следует вывод, что распределения  интервалов,  представленные на рис. 3 и аналогичные  им, обусловлены движением  измерительной  системы в неоднородном пространстве. Действительно,  для получения распределений,  имеющих четко выраженные  пики, воздействие на измерительную  систему должно быть: а) неоднородным; б) характер  этой неоднородности должен мало изменяться  в течение времени t₀.

Представленные  в настоящей статье результаты позволяют сделать следующий шаг и говорить  не просто  о неоднородности,  а  о структуре  пространства.  При  этом,  как следует из полученных результатов,  структура  реального  пространства  должна  иметь фрактальный характер.

Говоря  о структуре  пространства,  необходимо отметить  связь  между  законами  сохранения  и однородностью  пространства  [12]. Т. к. выполнимость  законов  сохранения энергии, импульса и момента импульса, связанных  с однородностью времени, однородностью и изотропностью пространства,  считается хорошо доказанной, то может возникнуть впечатление о противоречии вывода о наличии у пространства структуры  с выполнимостью законов сохранения. Но противоречие это кажущееся.  Действительно,  экспериментальная проверка законов сохранения, как и большинство физических  измерений, предполагает регистрацию хода во времени некоторых средних значений, в то время как, для используемого в настоящей работе метода макроскопических  флуктуаций исходным экспериментальным материалом  являются  не средние величины, а флуктуации относительно среднего. Образно говоря, если представить  исследование сохраняющейся величины,  как  неизменность  показаний  некоторого измерительного  прибора,  то исходным материалом  для  метода  макроскопических  флуктуаций является  еле заметное  дрожание – флуктуации – стрелки  прибора относительно  неизменного во времени среднего значения.  Подобные флуктуации всегда сопровождают  любое высокоточное измерение. Метод  макроскопических  флуктуаций, основан на  исследовании  подобия формы  пар гистограмм,  построенных на основе коротких  отрезков  временных  рядов  такого  рода флуктуаций в результатах измерений хода во времени параметра  некоторого процесса. Будучи  привязанным  к форме гистограмм,  он, поэтому, совершенно нечувствителен  ни к изменениям среднего, ни к изменению амплитуды самих флуктуаций, при условии, что эти изменения происходят за время большее, чем длительность  отрезка временного ряда, необходимого для построения гистограмм.  Измерения,  на основе которых получены результаты, представленные на рис. 3, как и любые другие измерения, используемые для исследования  феномена макроскопических  флуктуаций, выполняются  при неизменном или при равном нулю среднем значении измеряемой величины.

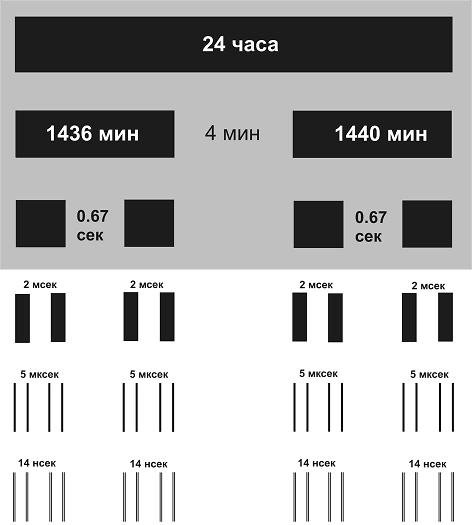
 Рис. 4. Схема  расщеплений  суточного цикла.  Серым прямоугольником  показаны расщепления, исследованные к настоящему времени.  Вне прямоугольника  показаны расщепления, которые предполагается  исследовать  в будущем.  Схема  построена на основе Табл. 1

 Вывод о фрактальной структуре пространства ведет к предположению, что подобная структура  должна  отражаться в спектрах  параметров  любых динамических  процессов, происходящих в нем. В настоящее время существует ряд работ, которые, на наш взгляд, говорят  в пользу  подобного предположения.  В первую очередь,  здесь необходимо от- метить [13, 14] посвященные феномену "многофазности", где был показан  полиэкстремальный  характер  отклика  различных  химико-биологических  систем на слабые внешние воздействия.  Фрактальность в спектрах  параметров  различных  природных  систем является  предметом рассмотрения концепции Global Scaling [15] в рамках которой реша- ется задача  вычисления фрактальных спектров для параметров  различных  природных систем, а также  развивается  ряд основанных на этом приложений.

Распределения  интервалов,  показанные  на рис. 3 могут быть представлены  в виде схемы,  рис.  4, где серым  прямоугольником  выделены  расщепления,  исследованные  к настоящему  времени.  Схема,  рис. 4, построена  на основе Табл.  1 и иллюстрирует  зависимость (2), являясь,  по сути, графическим  выражением  гипотезы о существовании расщеплений высшего порядка.  Исследование этих расщеплений требует все более высокочастотных  источников флуктуаций. В последней строке Табл.  1 выделены расщепления величина которых меньше 14 нсек (не показаны на рис. 4), исследование которых в настоящее время сталкивается с непреодолимыми техническими трудностями.

Изучение  расщеплений  t_n , n > 2, ведет к минимальному  масштабу,  на котором возможно исследование эффекта местного времени и через это к пониманию механизмов генерации флуктуаций, ответственных  за возникновение этого эффекта. Схема  расщеплений,  приведенная  на  рис.  4, возможно,  простирается  не только  в сторону расщеплений высших порядков  с n > 2, но и в сторону масштабов,  больших в сравнении с t₀:

t_m  = t₀/k_m   .                                                  (3)

Для  исследования  этого участка  пространственно-временной  шкалы  необходимо получение очень длинных записей. Рассмотрим  пример. Как уже упоминалось, при исследовании расщеплений высших порядков  наиболее перспективно использование расщеплений суточного периода, т. к., это позволяет получить максимальное,  в земных условиях t₀. Но, если предположить,  что суточный  период сам является  расщеплением  более длительного  периода,  то последний должен  быть порядка  года. Для  обнаружения  подобного периода необходим временной ряд флуктуаций продолжительностью не менее двух лет. Следующий шаг в сторону больших периодов (3) потребует запись не менее 720 лет. Приведенные оценки показывают,  что в настоящее время реальным представляется изучение  только  годичного  периода.  Его  изучение,  как  и исследование  расщеплений высших порядков, имеет принципиальное значение. Наличие расщеплений годичного периода можно рассматривать как свидетельство  того, что "солнечный"  и "звездный" периоды,  в действительности,  обусловлены некоторой глобальной  причиной, внешней, по отношению к солнечной системе. Отсутствие расщеплений, наоборот, может трактоваться  в пользу того, что на структуру  расщеплений пика местного времени в сильной мере влияют условия внутри Солнечной системы.

В настоящее время исследованы окологодичные периоды равные 525600 мин (календарный  год)  и 525939 мин (сидерический  год)  [16–17]. Исследование  расщеплений  во временной области получаемой  из (3) к настоящему  времени не проводилось.  Вопрос о том можно ли рассматривать полученные окологодичные  периоды как  расщепление годового периода также  остается открытым.

Необходимо отметить, что расщепление первого порядка  наблюдалось также  в опытах с вращением коллиматоров,  вырезающих  коллинеарные  пучки α-частиц, вылетающих при радиоактивном  распаде. При вращении коллиматоров  против часовой стрелки – имитации  суточного вращения  Земли  – также  наблюдалось  расщепление  на "звездный"  и "солнечный"   периоды,  длительность  которых  определялась  числом оборотов коллиматора в сутках [18–19].

Выражение  (1) на основе которого рассчитывалась Табл.  1 и строилась  схема расщеплений, рис. 4, в случае когда линия соединяющая  источники флуктуаций и вектор скорости измерительной системы не коллинеарны, может быть переписано в более общей форме:

t₀  = L₀/V   = L^. cos ф/V                                            (4)

где ф – угол между вектором скорости измерительной  системы и линией, соединяющей источники флуктуаций. Для  пары неподвижных  источников флуктуаций (4) дает раз- ность местного времени в местах проведения измерений при условии, что V – тангенциальная  скорость  измерительной  системы, обусловленная  вращательным движением Земли. Многочисленные экспериментальные исследования подтвердили несомненную выполнимость (4) для тех случаев, когда L₀  порядка десятков километров и больше [2–4,17]. Для  расстояний  порядка  метра эта зависимость  выполняется  только для  малых  в окрестности направлений север-юг и восток-запад [5, 20]. По нашему мнению, последнее обстоятельство также  может быть связано с фрактальной структурой,  присущей реальному пространству.  Действительно,  с ростом ф траектории  источников  флуктуаций 1 и 2, рис.  1, расходятся  и,  начиная  с некоторого  значения  ф  формы,  получаемых  от источников  флуктуаций гистограмм,  будут определяться  разными  неоднородностями. Что, в конечном итоге, приводит к исчезновению эффекта.

Предположение  о фрактальной структуре  пространства  ведет  к выводу  о зависимости величины k в (2) от скорости движения  измерительной  системы. Все описанные выше результаты были получены в условиях, когда V  обусловлена суточным вращением Земли. Для  случаев когда это не так,  нами получены предварительные  результаты, свидетельствующие  в пользу  предположения  о зависимости  получаемой  картины  расщеплений от скорости движения  измерительной  системы.

 Литература

 1. С. Э. Шноль, В. А. Панчелюга  Феномен макроскопических флуктуаций. Методика изме- рений и обработки  экспериментальных данных.  // Мир измерений, 2007, №6, с. 49–55.

2. С. Э. Шноль,  В. А. Коломбет,  Э. В. Пожарский, Т. А. Зенченко,  И. М. Зверева,  А. А. Ко- нрадов. О реализации дискретных состояний в ходе флуктуаций в макроскопических процессах

// УФН1998, 168 (10) с. 1129–1140.

3. С. Э. Шноль, Т. А. Зенченко,  К. И. Зенченко,  Э. В. Пожарский, В. А. Коломбет, А. А. Ко- нрадов.  Закономерное  изменение тонкой  структуры статистических распределений  как  след- ствие космофизических причин // УФН 2000, 170 (2), c. 214–218.

4. С. Э. Шноль.  Закономерные изменения  тонкой  структуры статистических распределе- ний в случайных процессах, как следствие арифметических и космофизических причин. Труды семинара  "Время,  хаос и математические проблемы"  выпуск  3, М., Книжный  Дом "Универ- ситет",  2004, с. 121–154.

5. В. А. Панчелюга,  С. Э.  Шноль.  О пространственной  анизотропии  выявляемой  при ис- следовании  "эффекта местного времени".  // Гиперкомплексные числа в геометрии и физике.

2006, №2 (6), Vol. 3 с. 188–193.

6.   V. A.   Panchelyuga,   S. E.   Shnol’.   Space-time   structure  and   macroscopic   fluctuations phenomena.  // Physical  Interpretation of Relativity Theory:  Proceedings  of International Meeting. Moscow, 2 – 5 July  2007 / Edited  by M. C. Duffy, V. O. Gladyshev,  A. N. Morozov, P. Rowlands.  - Moscow: BMSTU, 2007 - pp. 231–243.

7. В. А. Панчелюга,  В. А. Коломбет,  М. С. Панчелюга,  С. Э. Шноль.  Исследование  эффек- та местного времени на малых  пространственно-временных масштабах  // Гиперкомплексные числа в геометрии и физике,  1 (5), Vol. 3, 2006, c. 116–121.

8. Victor  A. Panchelyuga, Valery  A. Kolombet,  Maria  S. Panchelyuga and  Simon E.  Shnoll. Experimental Investigations of the Existence  of Local-Time effect on the Laboratory Scale and the Heterogeneity  of Space-Time.  // Progress  in Physics,  V.1, January, 2007, pp. 64–69. 

9. Г. Н. Рессел,  Р. С.  Дэган,  Д. К.  Стюарт.  Астрономия.  Т.  1. Солнечная  система.  М.-Л., ОНТИ,  1934 - 383 с.

10. А. А. Михайлов.  Земля  и ее вращение.  М., Наука,  1984 - 80 с.

11. Victor A. Panchelyuga, Simon E. Shnoll. A Study  of a Local Time Effect on Moving Sources of Fluctuations // Progress  in Physics,  July,  2007 V. 3, pp. 55-56.

12. Ландау  Л. Д., Лифшиц  Е. М. Механика.  М., Наука,  1988 - 216 с.

13. С. Э.  Шноль,  М. Н. Кондрашова, Х. Ф. Шольц.  О многофазном  характере  зависимо- сти аденозинтрифосфатной активности  актомиозина  и миозина от различных  воздействий.  // Вопросы медицинской химии, 1957, т. 3, вып. 1, с. 54–77.

14. С. Э. Шноль.  Многофазный характер изменений  свойств белка  под влиянием  слабых воздействий.  // Применение  радиоактивных изотопов  в  клинических   и экспериментальных исследованиях.  М., 1958, с. 199–208.

15. Raum  und Zeit. Special 1. Global Scaling. 2002 - 157 p.

16. S. E. Shnoll, K. I. Zenchenko, and N. V. Udaltsova.  Cosmophysical Effects in the Structure of Daily and Yearly Periods of Changes in the Shape of Histograms Constructed from the Measurements of 239Pu alpha-Activity. // Biophysics, 2004, v. 49, Suppl. 1, pp. 155–164.

17. Simon E. Shnoll. Changes in Fine Structure of Stochastic  Distributions as a Consequence of

Space-Time  Fluctuations. // Progress  in Physics,  2006, v. 2, pp. 39–45

18.  С. Э.  Шноль,  К. И.  Зенченко,  И. И.  Берулис,   Н. В.  Удальцова,   С. С.  Жирков, И. А. Рубинштейн.  Зависимость  "макроскопических флуктуаций"  от космофизических факторов. Пространственная анизотропия.  // Биофизика, 2004, т. 49 № 1 с. 132–139.

19.  S. E.   Shnoll,   I. A.  Rubinshtejn,  K. I.  Zenchenko,   V. A.  Shlekhtarev,  A. V.  Kaminsky, A. A.  Konradov,   N. V.  Udaltsova.   Experiments  with  rotating collimators  cutting   out  pencil  of alpha-particles at  radioactive  decay  of 239Pu  evidence  sharp  anisotropy  of space.  // Progress  in Physics,  2005, v. 1, pp. 81–84.

20. Victor  A. Panchelyuga, Simon E.  Shnoll.  On  the  Dependence  of a Local-Time  Effect on

Spatial  Direction  // Progress  in Physics,  2007, v. 3, pp. 51–54.