C.В.Ершков: Топологические аспекты динамического подобия в моделировании Времени

С. В. Ершков (г. Москва), 2003 г.

Существует множество концепций Времени, и все они не идеальны, хотя, может быть, некоторые и близки к истине – например, субстанциальная, реляционная, динамическая, пространственно-событийная и т.д.

Субстанциальная концепция определяет Время как особую субстанцию наряду с пространством, веществом, излучением и полем. Реляционная гипотеза толкует Время как отношение или систему универсальных устойчивых (математических) отношений между физическими событиями. Динамическая версия: Время – изменение порядка (качества) событий, при котором будущее превращается (схлопывается) в настоящее и прошлое. Наконец, пространственно-событийная концепция Времени: прошедшее и будущие времена существуют одновременно в общем пространстве событий.

Но наибольшей онтологической точностью отличается философское определение Времени: Время (основа Мироздания) – это имманентное (внутренне присущее) свойство мира, связанное с характером происходящих в нем изменений.

Что касается Времени-понятия как конструкта человеческого мышления [1], можно с уверенностью сказать следующее: для большей части точных наук Время имеет только лишь геометрическое свойство (как, например, в пространстве Минковского в приложении к ОТО Эйнштейна), или выступает как параметр.

Между тем, согласно основополагающим воззрениям Н.А. Козырева [2], это не совсем так (стр. 290): “…Время нельзя рассматривать оторванно от материи; образно говоря, Оно является грандиозным потоком, охватывающим все материальные системы Вселенной, и все процессы, происходящие в этих системах, являются источниками, питающими этот общий поток“.

Таким образом, мы можем рассматривать Время, - с точки зрения формально-логических построений, - как фронт непрерывных топологических преобразований, прокатывающихся миг за мигом по всем материальным системам Вселенной. Т.е. “Времени в будущем (относительно настоящего, текущего момента) попросту не существует - его ткань ткется сейчас существующими обстоятельствами всего окружающего нас Мира, и обрывается сразу по прошествии этого момента” [2].

При подобном подходе, ab inito нам следует сразу оговорить некоторые существенные моменты, а именно:

• Выбор пространства действия
(т.е. в каком именно пространстве нам предстоит работать - с афинным, конформным, etc. типом связности);
• В рамках какого класса алгебраических систем (группы, полугруппы, кольца, функторы и т.д.) мы будем изучать последовательности этих преобразований (в совокупности) в смысле выбора их структуры, согласованной с операцией композиции нескольких (последовательных) преобразований;
• Что является генератором преобразований данного типа (т.е., чем обусловлен выбор ядра оператора), включая характер непрерывности
;
• Какими правилами задается динамика изменения ядра оператора, и т.д.

Предваряя дальнейшее изложение, приведем некоторый теоретический материал, который будет нам крайне необходим при ответе на эти (и другие) вопросы:

Информационный блок № 1 (в соответствии с [3]):

Def. 1

Операторозначная функция T(s), удовлетворяющая уравнениям (наиболее общего вида, и определенная в области s ³ 0):

T (s+t) = T(s)* T(t), T(0) = I; s, t ³ 0 (1.1)

- называется полугруппой операторов.

Def. 2

Семейство {T(s)}, 0 £ s < ¥ , ограниченных линейных операторов в комплексном B-пространстве (банаховом пространстве) мы будем называть сильно непрерывной полугруппой, если:

(I) T (s+t) = T(s)* T(t), s, t ³ 0 ;

(II) T(0) = I; (1.2)

(III) " x Î B: функция T(s)* x непрерывна по s на оси [0, ¥ ).

Если, кроме того, отображение s ® T(s) непрерывно в равномерной операторной топологии, то семейство {T(s), s³ 0} называется полугруппой в B-пространстве, непрерывной в равномерной топологии.

Th. 1

Пусть {T(s)} – полугруппа, непрерывная в равномерной топологии. Тогда существует ограниченный оператор A, такой, что:

T(s) = exp {sA} , (1.3)

- при s ³ 0. Оператор A определяется формулой:

A = lim ((T(h) - I)/h) (1.4)

h ® 0

При Re (l ) достаточно больших резольвента A (или: резольвентная функция оператора A) может быть выражена через элементы полугруппы по формуле:

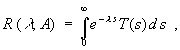(1.5)

- где R (l ; A) = (l I - A) ^-1 .

******************************

Информационный блок № 2 (в соответствии с [4]):

Def. 3

A simple definition of topology is that the study of properties that do NOT depend upon size or shape. (2.1)

Русский вариант:

Простое определение топологии (может быть дано следующим образом): это изучение таких свойств (объекта исследования), которые НЕ зависят от размеров или формы (этого объекта).

Далее (продолжая в соответствии с [4]):

The most fundamental topological properties is the number – the number of parts, the number of intersections, the number of links, the number of holes, the number of dimensions ….. Topological evolutions is the study of when and how these numbers change. [приводится в оригинале, без перевода]

******************************

Информационный блок № 3 (по аналогии с [5]):

Def. 4

Назовем автомодельностью в узком смысле следующее представление операторозначной функции T (t):

- где 0 £ t < ¥ , T(0) = I, a - показатель автомодельности.

Def. 5

Назовем автомодельностью в широком смысле следующее (рекурсивное) представление операторозначной функции:

- здесь, как и ранее, 0 £ t < ¥ , a - показатель автомодельности (в широком смысле), a .Î N; производная операторозначной функции определяется, как обычно, через предел отношения вариации функционала и d t (при d t ® 0) .

******************************

Теперь мы можем обозначить те самые существенные моменты, о которых шла речь выше:

• В качестве пространства действия (операторов) мы выберем
комплексное B-пространство (банахово пространство) [3], с афинным типом связности [3] (которое, при оснащении этого пространства соответствующей метрикой, может стать Гильбертовым); при этом каждое рассматриваемое отображение - непрерывно в равномерной операторной топологии в смысле (1.2);

• Мы будем изучать последовательности этих преобразований в рамках такого класса алгебраических систем как функторы
[1], которые, как известно, наделены полугрупповыми свойствами (1.1) в смысле их структуры, согласованной с операцией композиции нескольких (последовательных) преобразований [6];

• Генератор преобразований данного типа определяется в соответствии с (1.4)
; характер непрерывности обусловлен типом спектра всего семейства операторов, который при Re (l ) достаточно больших может быть определен при помощи (1.5);

• Динамика изменения ядра оператора задается (определяется) посредством соотношения (1.3), в котором единственной неопределенной и ничем (пока) не обусловленной величиной остается параметр
s ³ 0.

Мы намеренно опускаем (здесь и ниже) все подробности чисто математического изложения нашего подхода, поскольку это не есть цель данной работы, являющейся, по сути, всего лишь приглашением читателя к совместному размышлению над существом затронутой проблематики. Особенно ревностные блюстители строгости изложения могут ознакомиться с работой [7], где все это уже было проделано (подробнейшим образом) применительно к отображениям в оснащенных Гильбертовых пространствах для т.н. оператора эволюции (оператора Перрона-Фробениуса). Мне представляется также несложным и переход (без потери общности) от описания дискретных отображений к описанию непрерывных преобразований (описанию семейств операторов).

В этом месте, пожалуй, стоит сделать небольшое отступление, чтобы прояснить сущность и смысл этого чисто технически (казалось бы) введенного (выше) параметра s ³ 0. Дело в том, что существует работа Левича А.П. [1], из которой можно почерпнуть идею энтропийной параметризации процесса моделировании времени (см. [1]):

“Вслед за попытками распространения Второго начала термодинамики на масштабы Вселенной около века назад возникла идея количественного отождествления собственного возраста системы с уровнем ее энтропии. Плодотворность такого подхода полностью зависит от умения рассчитывать энтропию систем. …” И далее:

“Поскольку каждый допустимый морфизм переводит систему в новое состояние без изменения ее общей структуры, то число сохраняющих структуру морфизмов можно интерпретировать как число "микросостояний" системы, сохраняющих ее "макросостояние", т.е. общую структуру. Такая интерпретация позволяет назвать логарифм удельного числа преобразований состояния системы его обобщенной энтропией. … [и,далее:] … и измерять энтропийное время через количество допустимых структурой системы преобразований. А именно, приращение энтропии есть логарифм величины, показывающей во сколько раз изменилось это число преобразований.”

Мне представляется достаточно очевидным (фактом) удивительная схожесть высказанной А.П. Левичем идеи с идеей параметризации семейства эволюционных преобразований в равномерной операторной топологии в соответствии с (1.3). При этом параметр s ³ 0 есть не что иное, как энтропия рассматриваемой системы (претерпевающей эволюционные изменения).

Возвращаясь к работе [7], хотелось бы отметить следующий факт: автор приходит к мысли, что применительно (даже) к простейшим типам отображений (эволюционных преобразований), схема внутренних взаимосвязей в исследуемом объекте настолько сложна, что не представляется никакой возможности для точного предсказания динамической траектории отдельно рассматриваемого элемента (в заранее выбранном фрагменте изучаемого объекта).

Иными словами, по И.Пригожину, можно сделать следующий вывод:

1. Существует некий временной горизонт, за пределами которого описание подобных систем в терминах отдельных траекторий перестает быть применимым
;
2. В большинстве случаев можно выявить размер пула
(ансамбля) одинаковых элементов рассматриваемого объекта, при котором является возможным выписать для них какие-либо макро-модельные соотношения (уравнения), предсказывающие эволюцию этого пула на заданную глубину (в будущее), с заданной точностью и с заданным качеством (в смысле характера необратимости произошедших в этом будущем изменений).

Итак (подытоживая все вышесказанное), мы выдвинули следующую рабочую гипотезу: Время – процесс преобразования в особом пространстве с переменной, вариабельной топологией; причем характер вариабельности (изменчивости) топологии связан с характером происходящих преобразований (изменений) в этом пространстве. В общем и целом, это согласуется с философским определением Времени, которое мы давали выше (в начале).

Рассмотрим теперь операционный аспект выдвинутой гипотезы. Вспомним, в этой связи, о классической теореме Хана-Банаха [6] (теореме функционального анализа о продолжении действия линейного оператора с отдельно рассматривавемой области на все пространство действия оператора). Эта замечательная теорема дает нам все основания утверждать, что действие эволюционного оператора универсально на всем пространстве его действия (в смысле нормы). Это означает, что любое преобразование из рассматриваемой серии действует одинаково во всех областях рассматриваемого пространства, а именно: в каждой области пространства любой элемент этого пространства сдвинется не далее чем на заранее известную величину (что хорошо согласуется с опытными фактами существования светового барьера, по Эйнштейну).

При этом приобщенность исследуемых преобразований к топологии (в рамках сделанных предположений) дает нам право воспользоваться одним из свойств, обозначенных в (2.1), а именно тем что при изучении (выявлении) наиболее общих свойств этих преобразований (семейства операторов) мы должны помнить, что (в итоге) полученные результаты никоим образом не должны зависеть от каких-либо геометрических размеров (в т.ч., и по оси параметрического времени).

Подобное утверждение с необходимостью наталкивает на мысль об операционной автомодельности исследуемой модели (по аналогии со схожими моделями в различных областиях механики; см., например, работы [8-9]).

Это означает, что мы вправе воспользоваться представлением (3.2) для исследуемого семейства операторов как операционным обобщением соотношения (3.1) (с тем, чтобы уйти в конечном итоге от вхождения параметрического времени в явном виде в определяющие соотношения).

Далее вспомним еще раз Информационный Блок № 2 (см. выше): “The most fundamental topological properties is the number – the number of parts, the number of intersections, the number of links, the number of holes, the number of dimensions …”

Это означает, что в нашей модели нам также следует выделить некий главный параметр (“число”), который будет определять (задавать) тип топологии (в рассматриваемой системе). Таким числом может, безусловно, выступить показатель операционной автомодельности a (a .Î N). Именно этот параметр будет определять тип топологии, с которой мы имеем дело в настоящий момент (a .= 1: т.н. “плоская” топология, a .= 2: “цилиндрическая” топология, a .= 3: “сферическая” топология, и т.д. [далее идут N-мерные сферы]).

Теперь рекурсируем еще раз к определению топологии (2.1) (2-я его часть):

- при изучении (выявлении) наиболее общих свойств рассматриваемого семейства преобразований нам также нужно помнить, что все полученные результаты никоим образом не должны зависеть от “формы” изучаемых объектов. В нашем случае это означает, что нами решается задача со свободной границей (с т.н. свободными граничными, или свободными краевыми условиями).

В случае, если нами рассматриваются операторы с вещественным полем итоговых значений (функционалы), мы можем сказать, что (в таком случае) рассматриваемый в (3.2) оператор T(t) – есть число (правда, меняющееся в зависимости от изменяющихся граничных улсловий задачи), т.е. некий числовой инвариант изучаемой системы.

В качестве примера такого числового инварианта можно привести численность населения Земли N(t), исследование динамики которого было проведено С.П. Капицей в работе [10] “Феноменологическая теория роста населения Земли”. В ней он приводит феноменологически выведенное им (на основе анализа статист. данных, за разные периоды развития человечества) уравнение динамики численности населения Земли:

- где K – некая безразмерная константа роста (см. [10]).

Как объясняет сам Сергей Петрович (цитата): “Такая зависимость возникает потому, что при обмене и распространении информации происходит умножение числа ее носителей в результате разветвленной цепной реакции. … Очевидно, что обмен (и распространение) информации принципиально необратимые явления.”

Но мы теперь уже знаем, что данное соотношение - всего лишь одна из разновидностей эволюционных уравнений, выписанное в конечном числовом (функциональном) представлении, при a .= 2 (т.н. “цилиндрическая” топология возможных решений, с особенностью неограниченного нарастания решения {режима с обострением} “циллиндрического” типа).

В заключение хотелось бы также сказать несколько слов о (физическом) смысле автомодельных (операционных) соотношений (3.2). Согласно одноименной теореме (Th. Э. Нётер), любому инварианту динамической системы всегда соответствует некий закон сохранения; в нашем случае это означает следующее: если у системы существуют операционные инварианты (3.2), в системе выполняется закон сохранения топологического подобия (уподобления) любых иерархических подсистем данной динамической системы (при этом иерархические системы мы понимаем в соответствии с [1]).

Автор выражает глубокую признательность А.П. Левичу за плодотворные дискуссии и высказанные замечания в процессе переписки 2000-2001 гг., которые, безусловно, помогли автору выкристаллизовать с особой ясностью отдельные моменты для себя лично, а также нашли отражение в этой работе.

Список использованной литературы:

1. R.Khien. What is topology? // Page from Materials of “Cartan’s Corner” (http://www22.pair.com/csdc/car/carfre23/htm).
2. Седов Л.И.
Методы подобия и размерности в механике //М.: Наука, 1965 г.
3. Математический энциклопедический словарь под ред. Прохорова Ю.В. Раздел “Функторы” //
М.: “Большая Российская Энциклопедия”, 1995 г.
4. Г. Николис, И. Пригожин. Познание сложного // М.: Мир, 1990 г.
5. Ершков С.В., Щенников В.В. Об автомодельных решениях системы полных уравнений Навье-Стокса для случая осесимметричных закрученных течений вязкого сжимаемого газа // Журнал вычислительной математики и математической физики. 2001. Т. 41. № 7. С. 1117 - 1124.
6. Быркин А.П., Ершков С.В., Щенников В.В. Конически автомодельные решения уравнений Максвелла с кручением электро-магнитного поля // Материалы 3-его совещания по магнитной и плазменной аэродинамике в аэро-космических приложениях. М.: Институт высоких температур РАН. Апрель 2001. С. 124 – 125.
7. Капица С.П. Феноменологическая теория роста населения Земли // Успехи физ. наук. 1996. Т.166, N1