Почему на то, чтобы найти точное значение постоянной Планка, понадобилось 100 лет?
14-04-2017, 09:57. Разместил: Редакция ОКО ПЛАНЕТЫ

Перевод поста Майкла Тротта (Michael Trott) "An Exact Value for the Planck Constant: Why Reaching It Took 100 Years".
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Полине Сологуб за помощь в переводе и подготовке публикации
Содержание
— Некоторые мысли по случаю Всемирного дня метрологии в 2016 году
— Введение и немного обо мне
— От истоков метрической системы до сегодняшних дней.
— Увеличение числа констант
— Существующая система СИ и проблема килограмма
— Новая СИ
— Секунда
— Моль
— Кельвин
— Ампер
— Кандела
— Почему основных единиц измерения именно 7?
— Путь к изменению определения килограмма
Повествование ведется от имени Жана-Шарля де Борда.
Некоторые мысли по случаю Всемирного дня метрологии в 2016 году
Позвольте мне представиться:
Я человек науки и люблю точность.
Все это время я был где-то рядом.
Я забрал у людей фунт и туаз.
И я был рядом с Людовиком XVI
В минуты его сомнений и боли.
Я чертовски уверен в том, что метрическая рулетка,
Благодаря платиновым стандартам будет установлена раз и навсегда.
Я рад встрече с вами!
Надеюсь, вы угадали, как меня зовут?
Введение и немного обо мне
Если вы еще не догадались, я — Жан-Шарль де Борда: моряк, математик, ученый и член Академии наук. Я родился 4 мая 1733 года в городе Дакс во Франции. Две недели назад я отметил свой двести восемьдесят третий день рождения. А вот и я:
В моем родном городе в честь меня воздвигли памятник. Если вы будете неподалеку, задержитесь, чтобы посмотреть на него. Если вы не знаете, где находится Дакс, вот карта:
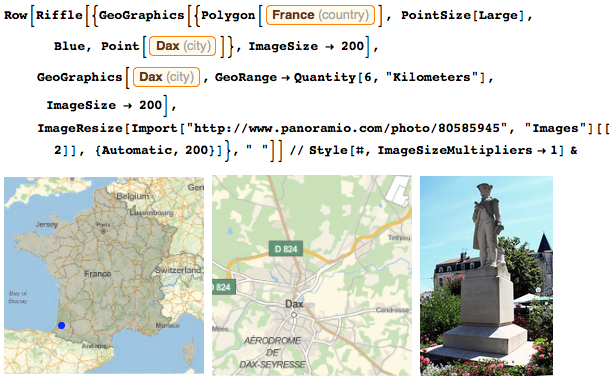
Когда я был мальчиком, Франция выглядела примерно так же, как сейчас. У нас было немного меньше территории с восточной стороны, но зато в Северной Америке моей стране принадлежал хороший кусок земли:
Я вел интересную жизнь. К 32 годам я провел много времени в открытом море, проводя научные исследования. Когда мне было сорок, я уже командовал несколькими кораблями в сражениях Семилетней войны (хотя большую часть своей жизни я все-таки посвятил науке).
Я умер 19 февраля 1799 года в Париже, и никто не знает, где моя могила (я-то знаю, конечно, но не могу рассказать об этом). Мое имя увековечено на северо-восточной стороне Эйфелевой башни:
На протяжении веков многие из моих коллег-французов, чьи имена присоединились к моему, говорили мне, что я заслужил место в Пантеоне. Однако вы не найдете меня ни там, ни на кладбищах Пер-Лашез, Монпарнас или Монмартр.
Но не это не дает мне покоя. Я скромный человек; не дает мне спать по ночам проблема с эталоном килограмма. Правда, скоро я смогу отдохнуть за все бессонные ночи.
Позвольте рассказать вам об этом.
Всю свою жизнь я занимался математикой, геометрией, физикой и гидрологией. Мне нравились измерения. Возможно, вы слышали о системе голосования (метод Борда) — это тоже моё изобретение. Я также значительно усовершенствовал периодический круг (repeating circle). Вот с этого-то и начинается моя история. Периодический круг сыграл решающее значение в определении точного размера Земли (обсуждение моего круга см. здесь).

Я жил во Франции во времена монархии. Это время было трудным для многих людей, и особенно — для крестьян. Отчасти так было потому, что торговля и коммерция были в упадке из-за отсутствия единой системы единиц измерения для страны в целом. Если вам нравится читать на исторические темы, я настоятельно рекомендую вам книгу Кула Люди и измерения — вы сможете представить себе, как обстояли дела с измерениями (прежде всего вес и размер) во Франции в 1790 году. Аналогичная ситуация сложилась и в других странах (см. доклад Иоганна Георга Траллеса о ситуации в Швейцарии).
В августе 1790 года по инициативе Людовика XVI я стал председателем Комиссии мер и весов. И до сих пор меня волнует тот факт, что через 1000 лет после инициативы Шарлеманя по унификации мер и весов началась новая работа в этом направлении. С помощью нашей комиссии была создана метрическая система, которая на сегодняшний день является международной системой единиц, сокращенно обозначаемой СИ (по-французски le Système international d'unités).
В комиссию также входили: Пьер-Симон Лаплас (уравнения Лапласа), Адриен-Мари Лежандр (полиномы Лежандра), Жозеф-Луи Лагранж (функция Лагранжа), Антуан Лавуазье (формулировка закона сохранения массы вещества), и Маркиз де Кондорсе (я всегда говорил Адриену Мари, что ему стоило бы заказать свой портрет, но он отнекивался, говоря, что слишком занят расчетами). За последние десятилетия Адриен-Мари подружился с Жаком-Луи Давидом, который написал целую коллекцию картин с ним; к сожалению, никто из смертных никогда не увидит их. Лагранж, Лаплас, Монж, Кондорсе и я входили в первоначальный состав команды (хотя в самом начале с нами был еще Жером Лаланд, а позже присоединился Луи Лефевр).
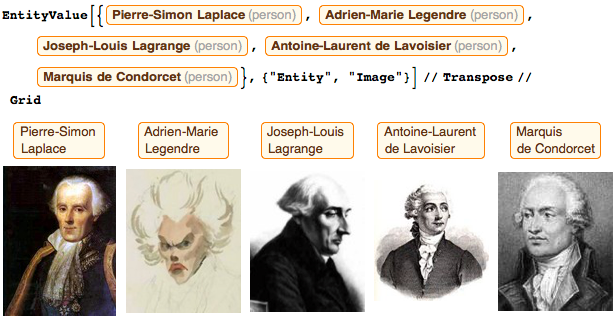
Трое из нас (Монж, Лагранж и Кондорсе) были похоронены или увековечены в Пантеоне. Я очень надеюсь на то, что в один прекрасный день к ним присоединится и Пьер-Симон, который этого заслуживает.
Как я уже говорил, французским гражданам сложно жилось в эту эпоху. Лаплас писал:
В использовании находится чудовищное количество единиц измерения; они неудобны для расчета, их трудно сравнивать; те затруднения, которые они производят в торговле, нельзя рассматривать, не признавая, что принятие измерительной системы (в которой единые ее части легко подвергаются расчету и которые получены по меньшей мере произвольно, причем единицы измерения должны быть указаны самой природой) станет одной из самых важных услуг, которые любое правительство может оказать обществу. Нация, внутри которой появится новая система мер, будет первой пожинать плоды ее преимуществ, а затем следовать ее примеру начнут и другие нации, для которых она, таким образом, станет благодетелем; медленное, но неотвратимое владычество разума, преобладающего над национальной ревностью, увенчает все преодоленные препятствия, противопоставляющие себя преимуществам.
Все пять математиков (Монж, Лагранж, Лаплас, Лежандр и Кондорсе) внесли исторически значимый вклад в математику. Их именами названы математические теоремы, структуры и операции:


В 1979 году Рут Инес Шампань написал диссертацию о влиянии пяти моих сограждан в создании метрической системы (чтобы узнать подробнее о вкладе Лежандра, см. статью Дорис Хеллман). Мне кажется, что на сегодняшний день математики в большинстве своем не интересуются больше единицами измерения, а движущей силой в этой области являются физики. Но я сделал, как в статье Теодора П. Хилла о методе объединения вероятностных распределений, позволяющем объединить знания из различных экспериментов (сразу скажу, что у нас на небе есть мгновенный доступ к arXiv. Скажу больше: прямое соединение с arXiv стало крупнейшим нововведением прошлого тысячелетия).
Наша задача состояла в том, чтобы создать унифицированные единицы измерения времени, длины, объема и массы. Нам нужны были такие единицы измерения, с помощью которых можно было бы измерить как крошечные, так и астрономического масштаба объекты. Принципы нашего подхода были хорошо обобщены Джоном Куинси Адамсом, государственным секретарем Соединенных Штатов, в книге 1821 года "Доклад по мерам и весам".

Первоначально мы (мы называли себя metric men) предложили лишь несколько префиксов: кило-, дека-, гекто-, деци-, санти-, милли- и мириа-, которая больше не используется (в некоторых старых книгах можно найти примеры использования приставки, означающей десять тысяч).
Эта идея использования префиксов довольно рано возникла в процессе разработки новых единиц измерения. Вот наши предложения 1794 года:

В свое время мы также использовали деми- и дабл- (деми-гектолитр (= 50 литров) или двойной декалитр (= 20 литров)).
Время, длина и масса, измеряемые в физике, химии и астрономии, охватывают более 50 порядков. И единицы, созданные нами в бурную эпоху французской революции, выдержали испытание временем:


В будущем для СИ, возможно, потребуется еще несколько префиксов. В недавно открытой обсерватории LIGO длина плеч интерферометра изменялась приблизительно на 10 йоктометров. Датчики массы с разрешением в йоктограммах уже существуют. Один йоктометр равен 10-24 метра. Человечество уже может измерять крошечные силы порядка зептоньютонов.
С другой стороны, астрономии нужны префиксы больше, чем 1024. И однажды они могут стать официальными.

Я человек строгих правил. Меня сводит с ума, когда в двадцать первом веке я вижу людей, которые не соблюдают правила использования префиксов СИ. Недавно я видел, как кто-то пишет на доске, что год состоит из из π декамегасекунд (π daMs):

Пускай это даже хорошее приближение (с отклонением всего 0,4%); только вот когда этот человек узнает, что не следует объединять префиксы?
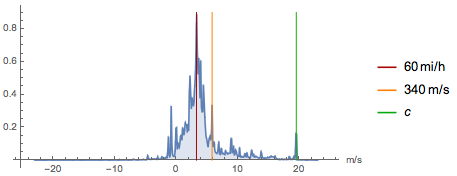
Технологический прогресс в течение последних двух столетий шел быстро. И префиксы мега-, гига-, тера- или нано-, пико- и фемто- в двадцать первом веке стали общеупотребительными. Ниже вы видите вероятностное распределение значений скорости. Некоторые скорости (например скорость звука или скорость света) используются чаще, чем другие, однако в функции распределения можно найти много локальных максимумов:
Вот отчет (который мы предоставили в марте 1791 года), давший начало метрической системе и в котором было описано концептуальное значение метра и килограмма. Он был подписан Лагранжем, Лапласом и Монжем (теперь он доступен даже через то, что современный мир называет «идентификатор цифрового объекта», или DOI, вроде 10.3931 /е-rarа-28950):

Большинство людей думает, что основание 10 тесно связано с метром, секундой и килограммом как единицами измерения. Однако мы решили использовать 10 в качестве основы для деления единиц только 27 октября 1790 года. Мы всерьез рассматривали 12 как основу, потому что делимость на 2, 3, 4 и 6 была удобна для торговли. Сегодня ясно, однако, что мы сделали правильный выбор. Лагранж был прав, когда настаивал на том, чтобы основанием стало число 10. Во время Французской революции мы не шли ни на какие компромиссы. А 5 ноября 1792 года я предложил перевод часов в десятичную систему счисления (Даламбер предложил это еще в 1754 году, подробнее см. эту статью). Человечество оказалось не готовым к таким изменениям; может быть, в двадцать первом веке десятичные часы, наконец, будут признаны гораздо более удобными, чем 24 часа, 60 минут и 60 секунд. Наши десятичные часы были прекрасны. Для меня стало настоящим сюрпризом, что человечество до сих пор делит угол на 90 градусов. В своем периодическом круге я делил прямой угол на 100 градусов.
Мы хотели сделать новые единицы измерения действительно равными для всех людей, а не основывать их, к примеру, на длине предплечья короля. В общем, «для всех времен, для всех народов» ( "À tous les temps, à tous les peuples). Теперь эта мечта исполнится.
Я уверен, что наступит день, когда предсказанное Менделеевым:
Давайте облегчим всеобщее распространение метрической системы, тем самым содействуя общему благосостоянию и желаемому будущему сближению народов. Оно придет не сразу, но постепенно и совершенно точно.
станет реальностью даже в тех 3 странах мира, которые не пользуются этой системой:

Единицы СИ стали законно использоваться в США с середины двадцатого века, когда обычные для США единицы измерения стали выводиться из определений основных единиц СИ. Граждане могут выбирать, какие единицы измерения они хотят использовать для торговли.
Мы также ввели десятичное исчисление в основу денежной системы, и наш франк был в обращении с 1793 по 2002 год. На сегодняшний день все страны имеют в обращении деньги, основанные на десятичной системе исчисления. Вот "разбивка" номиналов монет по странам:

Мы совершенно серьезно говорили про «всех людей», доказательством чему служит наша работа с нашими заклятыми врагами — Великобританией и новыми Соединенными Штатами (через Томаса Джефферсона лично) по созданию новой системы единиц измерения для всех основных стран. Но, как это часто бывает, в сражении политики и разума победила политика.
Я умер 19 февраля 1799 года, всего за несколько месяцев до первых успехов нашей группы. 22 июня 1799 года мой дорогой друг Лаплас произнес речь о создании новых единиц длины и массы еще до того, как новые образцы были доставлены в архив Республики (где они и находятся до сих пор).
В случае, если читатель заинтересовался моей богатой событиями жизнью, Жан Маскарт написал в 1919 году мою биографию, доступную теперь в виде репринтного издания.
От истоков метрической системы до сегодняшних дней
Двое из моих друзей: Жан-Батист-Жозеф Деламбр и Пьер Мешен отправились во Францию и Испанию для проведения измерений, чтобы определить метр как одну десятимиллионнную расстояния от Северного полюса до экватора Земли. Я рад, что миссия была утверждена. Когда Людовик XVI одобрил финансирование миссии, он уже находился под арестом. Мой дорогой друг Лавуазье назвал свою задачу «самой важной миссией, которая когда-либо была поставлена перед человеком".

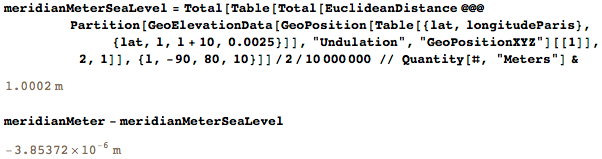
Если вы еще не прочитали книгу Кена Олдера Мера всех вещей, советую вам сделать это немедленно. Существует даже немецкий фильм о приключениях двух моих старых друзей. Вооруженные специальным инструментом, который я сконструировал для них, они проделали работу, результатом которой стало создание метра. Несмотря на то, что мы хотели установить длину метра, равную одной десятимиллионной длины половины меридиана, проходящего от полюса до экватора через Париж, я думаю, что сегодня это красивое определение исключительно концептуально. Мы не знали в то время, что Земля не совсем круглая, и ошибки в расчетах уплощения Земли привели к небольшой, но прискорбной ошибке в 0,2 мм. Вот длина половины парижского меридиана, выраженная в метрах:

Если бы учитывались все возвышенности (чего не сделали Деламбре и Мешен, потому что для этого им пришлось бы путешествовать вдоль всего меридиана, чтобы учесть каждую гору и холм!), и использовались 3D-координаты (в том числе высот местности), их метр в конечном итоге стал бы короче на 0,4 мм:

А вот профиль высоты по парижскому меридиану:
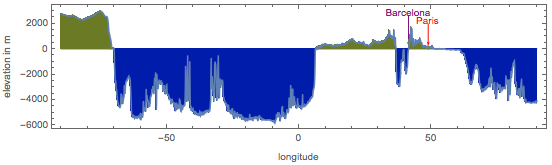
Из-за «фрактальности» поверхности Земли, если взять средство измерения ещё меньше, то ошибка значительно вырастет.
Метр окажется еще на 0,9 мм длиннее, если проводить измерения с помощью линейки длиной в несколько сотен метров:

Более реалистичным было бы следовать высоте уровня моря. Разница между полученными определениями метра составляет всего несколько микрометров:
Как минимум, меридиан должен был пройти через Париж (а не через Лондон, как предлагали некоторые британские ученые моего времени). Но в любом случае, нахождение длины меридиана было всего лишь ступенькой на пути к созданию образца метра. После того, как мы получили образец, меридиан нас больше не интересовал.
Вот набросок триангуляции, проведенной Пьером и Жан-Батистом за время их авантюрной шестилетней экспедиции. Благодаря Интернету и различным французским проектам по оцифровке — франкоязычные читатели, заинтересованные в метрологии и истории, могут теперь читать о полученных результатах онлайн и воспроизводить наши расчеты:
Часть Парижского меридиана (и Парижская обсерватория, отмеченная красным цветом) отмечены маркером: не пропустите их во время вашего следующего визита в Париж! Франсуа Араго переизмерил парижский меридиан. В 1804 году Лаплас получил от Наполеона деньги на повторное измерение меридиана для проверки и улучшения нашей работы:


Вычисляя секунду, мы отталкивались от продолжительности года. А килограмм в качестве единицы массы мы вывели из одного литра воды. Если какая-либо жидкость и является особенной, то это, конечно, вода. Лавуазье и я много спорили по поводу идеальной температуры. Вариантов было два: 0 °С и 4 °С. Первоначально мы думали о 0 °С, потому что лед легко увидеть. Но затем мы остановили свой выбор на 4 °С, потому что именно при такой температуре вода достигает максимальной плотности. Переход к 4 °C был предложен Луи Лефевром-Жане. Объем литра мы определили как куб одной десятой метра. После сравнения с высокоточными измерениями дистиллированной воды 1 кг оказался равным 1.000028 дм3 воды. Заинтересованный читатель может найти намного более подробную информацию о процессе проведения измерений воды и о создании исходной метрической системы. Более краткую историю на английском языке можно найти в недавней книге Уильямса.
Не хочу хвастаться, но мы также придумали само название «метр» (происходящее от греческого metron и латинского metrum), которое мы и предложили 11 июля 1792 года в качестве названия для новой единицы длины.
Чтобы соблюсти историческую точность, хочу отметить: пока я не вошел в небесные сферы, я всегда думал, что наша группа первой осуществила подобное. Я был поражен, когда вскоре после моего прибытия Я-син и Нанкин Юэ рассказали мне о своей экспедиции по определению единицы измерения длины, проходившей с 721 по 725 г., то есть более чем за 1000 лет до нашей.
Я очень рад, что мы определили метр таким образом. Первоначально идея состояла в том, чтобы определить метр с помощью маятника правильной длины с полупериодом в 1 секунду. Но я не хотел, чтобы какие-либо изменения, связанные с секундой, повлияли на длину метра. Так как определенного рода зависимости в системе единиц неизбежны, они должны быть сведены к минимуму.
В то время идея определять метр, основываясь на форме Земли, а секунду — на движении Земли вокруг Солнца, казалась хорошей. Это была даже лучшая идея, которую мы могли реализовать в то время. Мы не знали, как приливы и время изменили форму Земли, или как материки отдалялись друг от друга. Но мы верили в будущее человечества, верили в то, что точность измерений будет возрастать, хотя и не знали, что конкретно изменится. Это были первые наши шаги, предпринятые для точного измерения расстояний во Франции. На сегодняшний день у нас есть высокоточные геокарты:

Лучшие мастера моего времени плавили платину, и мы ковали бруски длиной в метр и образцы килограмма. Это было захватывающее время. Два раза в неделю я останавливался у Марка-Этьена Жанета — там, где он выковывал наши первые образцы килограмма. Плавление платины и придание ей формы не было еще отработано. Жанет — ювелир Людовика XVI — был настоящим мастером в работе с платиной (если быть совсем точным, с платиновыми губками). Всего за несколько лет до этого, 6 июня 1782 года, Лавуазье показал плавление платины в водородно-кислородном пламени будущему царю Павлу I; последний приезжал с визитом к Марии Антуанетте и Людовику XVI. В дальнейшем Этьен Ленуар сделал наш платиновый метр, а Жан-Николя Фортин — платиновый килограмм. Читателям, интересующимся историей платины, я рекомендую книгу Макдональдса и Ханта.
Платина — особый металл: для нее характерны высокая плотность и химическая инертность. Кроме того, она не такая мягкая, как золото. Лучшие на сегодняшний день эталоны килограмма сделаны из платино-иридиевого сплава (добавление иридия к платине действительно улучшает его механические свойства). Ниже приведено сравнение некоторых физических характеристик платины, золота и иридия:

Это звучит просто, но в то время лучшие ученые провели бесчисленное количество часов в расчетах и экспериментах, чтобы найти лучшие материалы, лучшие формы и наилучшие условия для определения новых единиц. Но и новый образец метра, и новый килограммовый цилиндр были макроскопическими телами. Все макроскопические артефакты трудно транспортировать (мы разработали специальные футляры для перевозки); они изменяются совсем немного даже спустя 100 лет использования, абсорбции и десорбции, нагревания и охлаждения. В результате технического прогресса девятнадцатого и двадцатого веков стало возможным измерять время, массу и длину с точностью до одной миллиардной. А измерение времени может быть сделано в миллиард раз лучше.
Я до сих пор очень хорошо помню, что после того, как мы сделали новые эталоны длины и массы, Лавуазье сказал: "ничего более величественного и простого не выходило из рук человека". Я и сейчас так думаю.
Наша цель состояла в том, чтобы создать единицы измерения, удобные для всех. Наш девиз звучал как: «для всех народов — во все времена». Мы разместили копии метра по всему Парижу, чтобы все знали, какой именно длины он был (в следующий раз, когда вы посетите Париж, не забудьте посмотреть на mètre étalon рядом с Люксембургским дворцом). Вот на этой фотографии, которую я недавно нашел, показано, как заинтересованно немецкий турист изучает историю одного из немногих оставшихся эталонов метра:

Это было захватывающее время (пускай даже меня не было рядом, когда комиссия завершила эту работу). Наши единицы измерения использовались в большинстве европейских стран в девятнадцатом и большей части двадцатого века. Мы создали метр, секунду и килограмм. Позже к результатам нашей работы были прибавлены еще четыре основные величины (ампер, кандела, моль и кельвин). С этими обновлениями метрическая система прослужила человечеству более двухсот лет.
На графике ниже изображен резкий взлет частоты использования в книгах слов килограмм, километр и килогерц, случившийся после Метрической конвенции 1875 года:

Мы определили только метр, секунду, литр и килограмм. Сегодня в СИ входит гораздо больше единиц: беккерель, кулон, фарад, грэй, генри, герц, джоуль, катал, люмен, люкс, ньютон, ом, паскаль, сименс, зиверт, тесла, вольт, ватт и вебер. Вот список размерных соотношений (никакого физического смысла не подразумевается) между производными единицами:


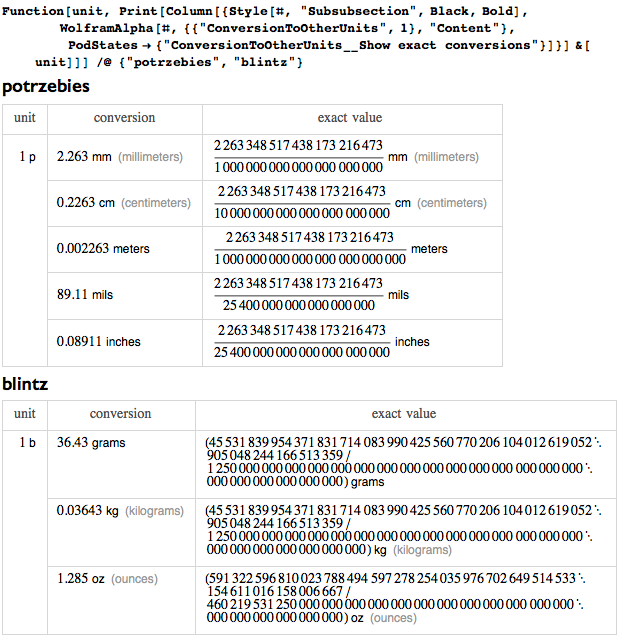
Многие именные единицы, добавленные уже после моей смерти, были связаны преимущественно с электрическими и магнитными явлениями, которые еще не были известны при моей жизни. И хотя я в целом серьезный человек, я люблю шутки и каламбуры. Однако мне не по душе, когда шутят над единицами измерения. Например, существует такая система с единицами измерения: potrzebie, ngogn, blintz, whatmeworry, cowznofski, vreeble, hoo и hah (система введенная Дональдом Кнутом (Knuth's Potrzebie system of units)). Мало того, что их имена бессмысленны, — их значения так же не имеют смысла:
Или посмотрите на предложение Макса Петерсона касательно единиц измерения для биологии. Названия единиц и префиксы могут показаться смешными, но для меня единицы измерения — слишком серьезный предмет:

Эти названия единиц даже не рифмуются ни с одним из имен собственных:


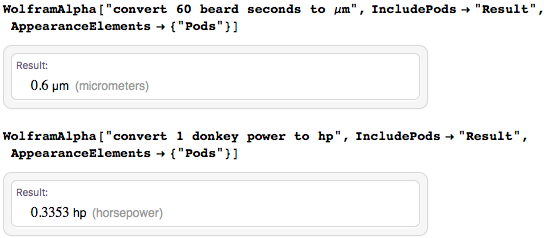
Повторюсь: я люблю иногда пошутить (даже с единицами измерения), но должно быть ясно, что это не всерьез:
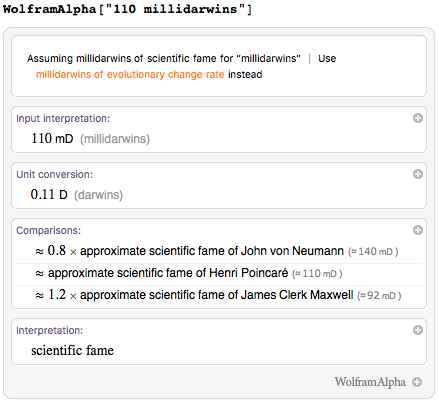
Есть еще явно ненаучные единицы, — такие, как «helens» для красоты, «puppies» для счастья или «darwins» — для славы:


Я очень горжусь тем, что единицы СИ — это не мертвые бумажные символы, а инструменты, которые регулируют современный мир. Хотя я и не любитель комиксов, мне понравилось недавнее представление базовых единиц измерения в виде супергероев от Национального института стандартов и технологий (NIST):

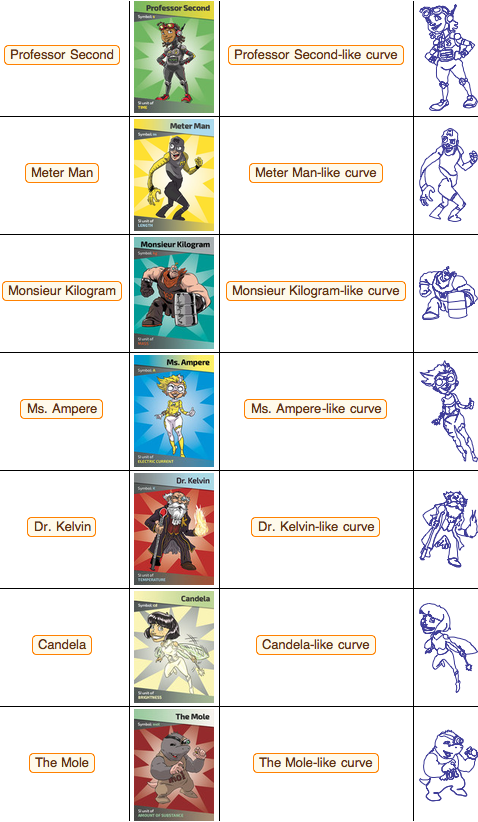
Обратите внимание: чтобы почтить вклад пяти великих математиков в создание метрической системы, кривые в крайнем правом столбце даются в виде математических формул; например, для д-ра Кельвина у нас имеется следующая чисто тригонометрическая параметризация:

Таким образом, мы можем "построить" доктора Кельвина:
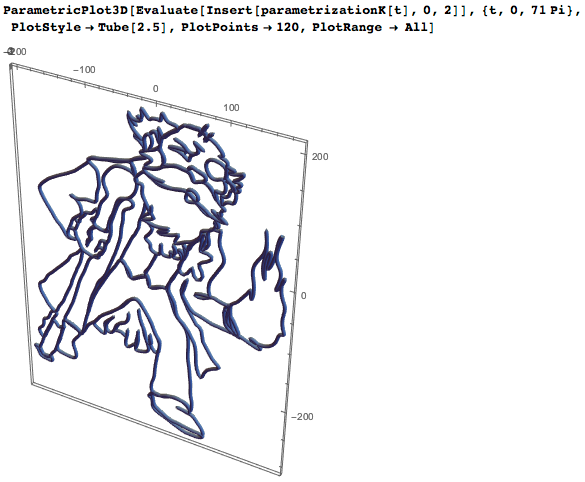
Наличие таких персонажей в параметрической форме — это очень удобно: когда моя семья собирается вместе, малыши занимаются своим любимым делом: раскрашивают супергероев. Я просто распечатываю кривые, а затем дети могут развлекаться (я позаимствовал эту идею пару лет назад из раскраски от NCSA).

И всякий раз, когда выходит новый эпизод, все собираются вместе, чтобы посмотреть его. Как вы понимаете, последний эпизод — наш любимый. Ходят слухи, что предстоящая книга Возвращение метрологов (2018 — станет идеальным годом!) дополняет существующую книгу.
Я рад, что важность измерений и основной метрической системы отмечается на Всемирном дне метрологии — 20 мая.
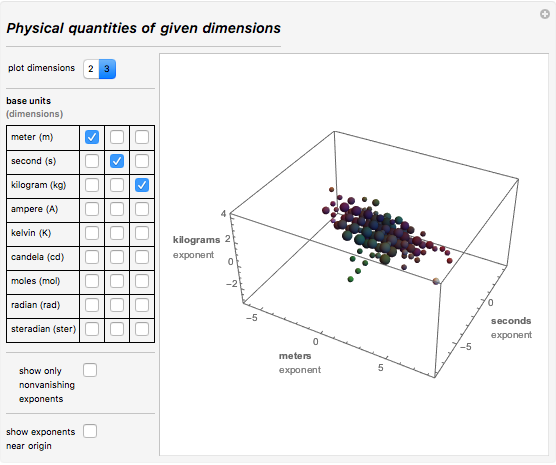
В то время, когда я жил, люди измеряли только товары: зерно, картофель и другие продукты, а также вино, ткани, дрова и т.д. Так что моей стране действительно нужны были единицы длины, площади, объема, и, конечно, единицы времени. Я всегда знал, что важность измерений будет со временем только расти. Весьма примечательно, что только спустя 200 лет после того, как я вошел в небесные сферы, число измеряемых физических величин достигло нескольких сотен. На сегодняшний день только Международная организация стандартизации (ISO) определяет и описывает, какие физические величины следует использовать. Ниже приводится изображение интерактивной демонстрации (загрузите документ вверху этого поста, чтобы взаимодействовать с ним), на котором графически показаны размерности физических величин для подмножеств выбранных единиц измерения. Сначала выберите два или три измерения (основные единицы измерения). Затем на графике будут показаны сферы с размерами, пропорциональными количеству различных единиц измерения, которые получаются из выбранных. Например, в случае с «метром», «секундой» и «килограммом» диаграмма показывает такие единицы измерения физических величин, как импульс (кг1 м1 с-1) или энергию (кг2 м1 с-2):
Вот отрывок кода, который я использовал для создания этих графиков. Это все физические величины с размерностями L2 M1 T-1. Последняя из них является слегка экзотической единицей из электродинамики
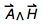 :
:
На сегодняшний день с помощью смартфонов обычные люди замеряют множество физических величин. Я бы сказал, «измерения рулят». Или как мой дорогой друг Уильям Томсон любил говорить:
… Когда вы можете измерить то, о чем вы говорите, и выразить это в цифрах, — вы знаете что-то об этом; но когда вы не можете выразить это в цифрах, ваши знания скудны и неудовлетворительны; это может быть начало знания, но, независимо от предмета, вы вряд ли добрались до стадии науки.
Вот графическая визуализация физических величин, которые измеряются с помощью наиболее распространенных измерительных приборов:

Электрические и магнитные явления только набирают популярность. Электромагнитные эффекты, связанные с физическими величинами, стали популярными гораздо позже:

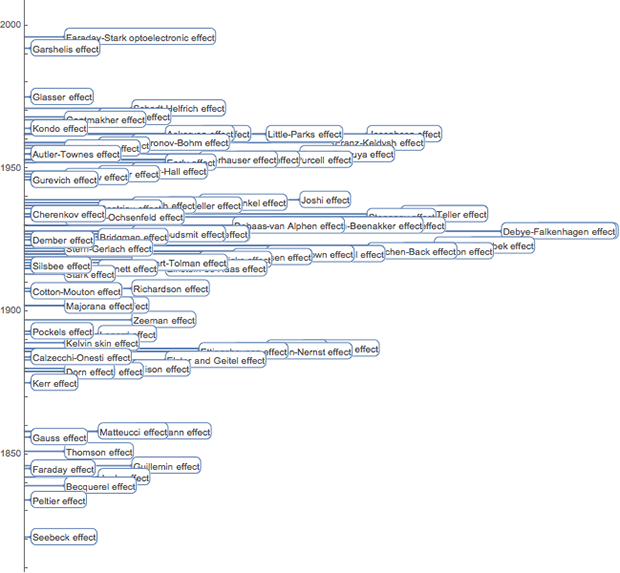
До сих помню, как я был взволнован, когда во второй половине ХIХ века и в начале ХХ века были обнаружены различные физические величины электромагнетизма и поняты их взаимосвязи (и не забудьте про недавнее добавление мемристора). Ниже представлена диаграмма, демонстрирующая наиболее важные электрические/магнитные физические величины qk, которые имеют отношения вида qk = qi qj:

С другой стороны, я был уверен, что явления, связанные с температурой, вскоре будут поняты в полной мере. И действительно: всего 25 лет спустя Карно доказал, что теплота и механическая работа эквивалентны. Теперь я также знаю о замедлении времени и сокращении длины в соответствии с теорией Эйнштейна. Однако человечеству до сих неизвестно, является ли движущееся тело более холодным или более теплым, чем неподвижное (или они имеют одинаковую температуру). Каждую неделю я слышу от Уилларда Гиббса о смежной теме отрицательных температур. А в последнее время он был очень взволнован новостью о том, что значение максимальной температуры для данного объема V выражается через фундаментальные константы:

Максимальная температура одного кубического сантиметра:

Увеличение числа констант
Спустя продолжительное время после моей физической смерти лучшие ученые в области физики 19-го и начала 20-го вв. — Джеймс Максвелл, Джордж Стони и Макс Планк (и Гилберт Льюис) обсуждали единицы измерения времени, длины и массы, основанные на неизменных свойствах микрочастиц и связанных с фундаментальными физическими константами (скорость света, гравитационная постоянная, заряд электрона, постоянная Планка и т.д.):
Максвелл писал в 1870 году:
Тем не менее, размеры нашей Земли и время ее вращения характеризуются завидным постоянством. Земля может сжиматься, охлаждаясь, или расширяться за счет слоя метеоритов, падающих на нее, или скорость ее вращения может ослабиться, — и все же она будет такой же планетой, как и раньше.
Но молекула, скажем, водорода, если ее масса или время ее вибрации изменятся хотя бы немного, больше не будет молекулой водорода.
Итак, если мы хотим получить стандарты длины, времени и массы, которые должны быть абсолютно постоянными, мы должны искать их не в размерах, или движении, или массе нашей планеты, но в длине волны, периоде вибрации и в абсолютной массе этих нетленных, неизменных и совершенно подобных молекул.
Когда мы видим, что здесь, как и в звездном небе, присутствует неисчислимое множество маленьких тел одинаковой массы, не разделяющихся дальше и вибрирующих одновременно много раз в секунду, и когда мы размышляем о том, что никакая сила в природе не может теперь изменить массу или период любой из них, — вот тогда мы, кажется, продвинулись по пути естественного знания к одной из тех точек, в которых должны принять ту веру, благодаря которой мы понимаем, из чего состоит все видимое.
В то время, когда Максвелл писал это, я уже давно находился на небе, и когда я прочитал это, я аплодировал ему (пускай у меня и оставался еще некоторый скептицизм по отношению ко всем идеям, идущим из Великобритании). Я знал, что это был путь вперед, позволяющий увековечить единицы, созданные нами во время Французской революции.
Существует много физических констант. И не все они известны с одинаковой точностью. Вот некоторые примеры:

Преобразование значения констант с известной ошибкой в числа произвольной точности удобно для следующих вычислений. Связь между доверительными интервалами и количеством цифр задается следующим образом: число произвольной точности, которое соответствует v ± δ — это число v с точностью -log10(2δ/v). И наоборот: если дано число с произвольной точностью, мы можем воссоздать v ± δ:

После точно определенных констант постоянная Ридберга с ее 11-ю знаками после запятой выделяется среди других констант своей точностью. На другом конце спектра находится G — гравитационная постоянная. По крайней мере раз в месяц Генри Кавендиш останавливается у меня с очередной идеей о том, как построить настольный прибор для измерения G. Иногда в основе его идей лежат холодные атомы, а иногда — сверхпроводники. Если бы он мог еще общаться с живыми, он писал бы еженедельные комментарии в Nature. Чуть больше года назад Генри был обеспокоен необходимостью проводить свои измерения и зимой, однако позже он узнал, что сезонной зависимости у значения G не существует. Предварительный дедлайн для Big G Challenge был всего четыре дня назад. Я думаю, что на следующей неделе я уже буду смотреть с небес на предварительные эксперименты.
Есть и другие физические константы. Некоторые из них более фундаментальные, чем другие, однако сейчас я не хочу вдаваться в подробное обсуждение этой темы. Заинтересованному читателю понравятся статьи Леви Леблонда (и вот еще), и эта статья, и вот эта, и ставшая уже классикой статья Даффа-Окуня-Венециано. Для создания единиц измерения на основе физических констант различия между классами физических констант не столь актуальны.
Абсолютные значения констант и их отношение к Раю, Аду и Земле — отдельная тема. Эта тема бурно обсуждается смертными (также см. эту статью). Некоторые численные совпадения (?) просто озадачивают:

Конечно же, с использованием современных математических алгоритмов вроде lattice reduction мы можем заниматься нумерологией числовой части физических констант:

Например, как мы можем вывести число π на основе фундаментальных констант?

Или давайте посмотрим на мой любимое число, скажем 10 — математическую основу метрической системы:

С учетом имеющегося набора констант, существует много способов выведения единицы измерения из заданной единицы. На сегодняшний день существует так много физических констант, что вы должны действительно интересоваться ими, чтобы не потеряться в этом множестве. Вот некоторые из наименее известных констант:

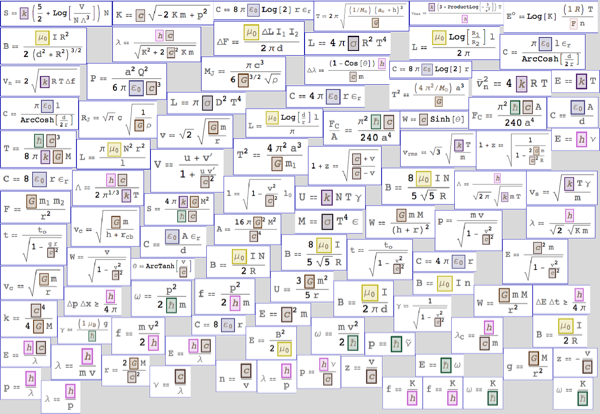
Физические константы появляются во многих уравнениях современной физики. Вот подборка из 100 простых физических формул, содержащих фундаментальные константы:
Конечно, более сложные формулы также содержат физические константы. Например, в формуле гравитационных потенциалов различных объектов появляется гравитационная постоянная (конечно же!) различных объектов, — например, для потенциала отрезка и потенциала треугольника:

Мой друг Мауриц Корнелис Эшер любит такие формулы. Недавно он показывал мне вариации нескольких его 3D-картин, которые показывают эквипотенциальные поверхности всех объектов в изображениях с помощью триангуляции всей поверхности, а затем применяется приведенная выше формула. На графике показан урезанный вариант двух эквипотенциальных поверхностей:

Я часто останавливался у Маурица Корнелиса, и почти всегда он был в компании — как правило, Альбрехта Дюрера. Они оба — любители играть с формами, поверхностями и многогранниками. Они деформируют их, инвертируют и многое другое. Альбрехт также любит применять технику сглаживания по отношению к гравитационным потенциалам, но часто делает это только с краев. Вот как выглядят эквипотенциальные поверхности твердых тел у Дюрера:

А вот визуализация формул, содержащих сα–hβ-Gγ в пространстве степеней αγβγγ. Размер сфер пропорционален числу формул, содержащих сα · hβ · Gγ; передвигая курсор по сферам, вы можете увидеть в прилагаемом документе фактические формулы. Мы рассматриваем положительные и отрицательные степени одинаково:

А вот одна из моих любимых формул для квантово-скорректированной силы притяжения, которая содержит три мои любимые константы: скорость света, гравитационную постоянную и постоянную Планка:

Формула энтропии черной дыры — тоже одна из моих любимых. В дополнение к с, h и G она содержит постоянную Больцмана:
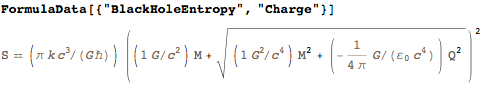
И, конечно же, поправка второго порядка к скорости света в вакууме в присутствии электрического или магнитного поля из-за фотон-фотонного рассеяния (без учета поляризационного-зависимой постоянной). Даже в очень больших электрических и магнитных полях изменения скорости света очень малы:
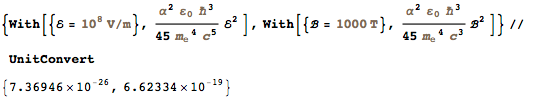
В то время, в котором я жил, мы не понимали физический мир до такой степени, чтобы придумать естественные единицы. Так продолжалось до 1874 г., когда Стони впервые представил в своей лекции естественные единицы измерения в Научной ассоциации Британии. Позже, в своих лекциях 1906-07 гг., Планк уже широко использовал единицы измерения (ныне называемые планковскими), уже введенные им в знаменитой статье 1900 года "Анналы физики". К сожалению, в обеих этих системах единиц измерения гравитационная постоянная G занимает видное место. На сегодняшний день мы не можем измерить ее достаточно точно. В результате значения планковских единиц в СИ имеют только около четырех знаков после запятой:

Эти единицы измерения не годились для ежедневного использования, так как были либо слишком малы, либо слишком велики по сравнению с теми длинами, площадями, объемами и массами, с которыми люди сталкивались ежедневно. Но почему бы не построить единицы измерения, пригодные для ежедневного использования, на основе таких неизменных микроскопических свойств?
(Примечание: самое смешное, что в последние 20 лет Макс Планк снова сомневается в том, что его постоянная h действительно фундаментальная. Он надеялся, что в 1900 году получит ее значение из полуклассической теории. Теперь он надеется вывести его из некоторых голографических аргументов. Или по крайней мере он думает определить величину h/kB. Я не знаю, добьется ли он успеха, но кто знает? Он умный парень).
На сегодняшний день известны многие точные и приближенные соотношения между фундаментальными константами. Некоторые могут быть обнаружены в будущем. Может ли постоянная Планка потенциально быть связана с размерами Вселенной?

Вот еще формула Бека, демонстрирующая замечательное совпадение:

Тем не менее, в мое время никто и подумать не мог о том, чтобы выразить высоту жирафа посредством фундаментальных констант. Поэтому я был так поражен, когда лет 10 назад, просматривая новые препринты arXiv, нашел формулу для определения высоты самого высокого живого существа, которое может бегать, полученную доном Пэйджем. Он получил высоту жирафа (брахиозавр и завропосейдон не в счет, потому что они не могут бегать) в терминах фундаментальных констант с погрешностью, не более чем в 2 раза, — я считаю, это просто удивительно:

В 1983 году Пресс, Лайтман, Пайерлс и Голд выразили максимальную скорость движения человека (см. также более ранние статьи Пресса):

Мне также очень понравилась работа Барроуса и Острайкера о выражении размеров различных астрономических объектов только через фундаментальные константы. Например, для массы типичной галактики мы получаем следующее выражение:
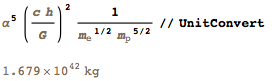
Это значение находится в пределах небольшого отклонения от массы Млечного Пути:

Однако вернемся к нашим единицам измерения и быстро перемотаем время на 100 лет вперед, оказавшись сразу во второй половине ХХ века: идея базирования единиц на свойствах микроскопических объектов получала все большее распространение.
В 1967 году секунда была определена как время, равное 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133, находящегося в покое, а метр в 1983 году был определен как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1/299 792 458 секунды. Чтобы быть точным, это определение должно быть реализовано в состоянии покоя, при температуре 0 К и на уровне моря. Пренебрежение уровнем моря может привести к значительным ошибкам измерения; ядро Земли почти на 2,5 года моложе ее поверхности из-за различий в гравитационном потенциале.
Теперь определения секунды и метра как единиц измерения действительно равны для всех людей. Равны не только для людей на Земле, но и в будущем, и далеко, далеко от Земли для любого инопланетянина (однажды периоды цезия наверняка заменят большим числом периодов другого элемента, но это не отменит универсальности данной единицы измерения).
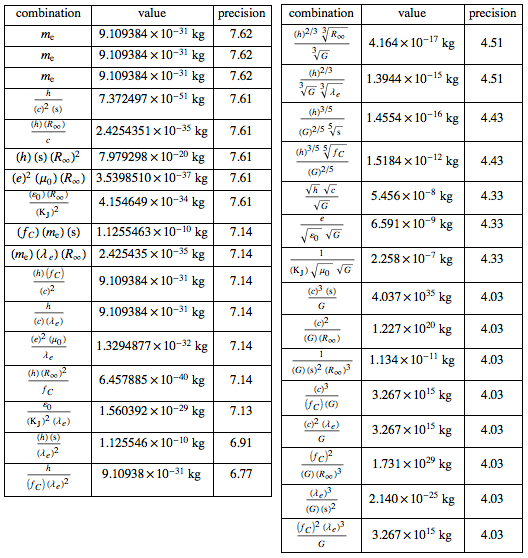
Однако, если мы хотим обосновать все единицы через физические константы, какие из них мы должны выбрать? Существует множество способов выражения основных единиц измерения через набор констант. Используя константы из приведенной выше таблицы, можно получить тридцать (тридцать!) способов, как объединить их для получения единицы массы:

Из-за различной точности самих констант их комбинации также будут отличаться в смысле точности (и числовых значений тоже):
Вопрос в том, какие константы должны быть выбраны для определения единиц метрической системы? Необходимо учитывать многие аспекты: от точности и практичности до общей согласованности. Мы хотим, чтобы наши формулы выглядели как F = m а, и не содержали явных чисел вроде формулы времени приготовления индейки на День Благодарения (предполаем сферическую индейку):

Или в формуле PLANK для расчета мощности двигателя в лошадиных силах:

Здесь, на небе, мы не можем использовать физические компьютеры, так что я рад, что могу пользоваться виртуальным Wolfram Open Cloud для своих расчетов и экспериментов. Я много часов играл с интерактивными единицами-константами (ниже), и полностью согласен с выбором, сделанным Международным бюро мер и весов (МБМВ): скорость света, постоянная Планка, элементарный заряд, число Авогадро и постоянная Больцмана. Я показал предварительный вариант этой статьи для блога Эдгару, и он был очень рад увидеть эту таблицу, в основе которой лежит его старая статья:

Хочу отметить, что самая популярная физическая константа — постоянная тонкой структуры — не слишком полезна для построения единиц измерения. Учитывая ее безразмерность, понятно, почему она не может быть сопряжена с единицей измерения. Хотя, конечно, это одна из самых важных физических констант в нашей Вселенной (наверное, ее превосходит только простая целая константа, описывающая, сколько пространственных измерений есть в нашей вселенной). Часто различные безразмерные комбинации могут быть найдены из заданного набора физических констант благодаря отношениям между константами: таким, как с2 = 1/(ε0 μ0). Вот некоторые примеры:

Наверное, нет ни одной другой константы, которую мы с Полем Дираком обсуждали бы так подробно в течение последних 32 лет, чем постоянная тонкой структуры α = е2/(4πε0ħс). И, хотя мы здесь регулярно встречаемся с Господом в дружественной и продуктивной атмосфере, он по-прежнему отказывается открыть нам замкнутую форму α. И он даже не расскажет нам, выбрал ли он то же значение для всех времен и мест. Что касается соответствующей темы значений выбранных констант, то он также отказывается обсуждать тонкую настройку и альтернативные значения. Он говорит, что в один прекрасный день мы все узнаем. Он очертил некоторые границы, но они были не намного более точными, чем те, которые мы знаем благодаря открытиям на Земле. Так что, как и ныне живущие смертные, теперь мы должны просто угадывать математические формулы:

Или комбинации констант:
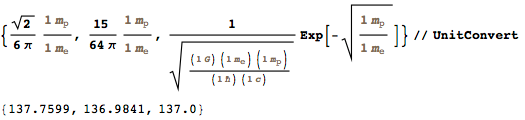
А вот одно из моих любимых совпадений:

И еще несколько:

Повышение значимости и широты использования физических констант хорошо отражено в научной литературе. Вот график, демонстрирующий, как часто (количество публикаций в год) появляются наиболее распространенные константы в научных публикациях от издательства Springer. Логарифмическая вертикальная ось показывает экспоненциальный рост упоминаний физических констант:

В то время, как фундаментальные константы всюду встречаются в физике и химии, упоминания от них в газетах, кино или рекламе практически отсутствуют. Я был очень рад видеть новую колонку под названием Мера за меру в журнале Nature.
Я надеюсь, что еще до переопределения мы увидим новые интересные видеоигры, которые позволяют игрокам изменять значения C, G и h, чтобы увидеть, как меняется мир вокруг нас в зависимости от значений констант. Мне очень хочется поиграть в такую игру. При больших значениях h можно построить мир с котами Шредингера. А вот еще с помощью игры можно познакомить с константами детей раннего возраста. Именно такой является игра о приключениях мистера Томпкинса:
Было бы интересно посмотреть, насколько быстро и эффективно человеческий мозг будет адаптироваться к возможной жизни в другой Вселенной. Первоначальные исследования обнадеживают. Но, возможно, наш мир и наше небо действительно детально проработаны.
Существующая система СИ и проблема килограмма
Кроме метра и килограмма, в современную СИ включены и другие единицы измерения. Ампер определяется как сила неизменяющегося тока, проходящая по двум параллельным прямолинейным проводникам бесконечной длины, кельвин — через термодинамическую температуру тройной точки воды, моль — через килограмм и углерод-12, и кандела — через излучение абсолютно черного тела. Если вы никогда не читали брошюру СИ, я настоятельно рекомендую вам сделать это.
Два бесконечно длинных провода, — это, безусловно, уровень макроскопический. И для поддержания состояния тройной точки воды необходимо макроскопическое ее количество. Это не идеально, но нормально. Углерод-12 — это уже микроскопический уровень. Излучение абсолютно черного тела — снова представляет собой ансамбль микрообъектов. Таким образом, кое-что из текущей СИ достигает в некотором смысле целей Максвелла.
Однако главной причиной моей бессонницы в течение последних 50 лет стал… килограмм. Когда я думал о нем, у меня начинала болеть голова и меня мучили ночные кошмары.
В 1799 году (это еще и год моей смерти) был создан первый прототип килограмма — маленький платиновый цилиндр. Он был около 39,7 мм в высоту и 39,4 мм в диаметре, и в течение 75 лет он служил эталоном килограмма. Он был создан из кованой платиновой губки, сделанной Джанети. Миллер приводит много деталей этого образца килограмма. Они находятся сейчас в национальных архивах. В 1879 году компания Johnson Matthey с помощью новых технологий плавления сделала материал для трех новых образцов эталона килограмма. Из-за несколько более высокой плотности эти килограммы были немного меньше по размеру (на 39,14 мм ниже). Цилиндр был назван KIII и стал новым международным прототипом килограмма
 . Вот последняя фраза из определения международного прототипа килограмма 1885 года:
. Вот последняя фраза из определения международного прототипа килограмма 1885 года:
Несколько эталонов килограмма выборочно сравнили с нашим оригинальным эталоном; если вас интересуют детали измерений, см. эту книгу. Все три образца оказались менее чем на 1 мг легче исходного килограмма. У одного образца разница оказалась менее 0,01 мг по сравнению с первоначальным килограммом. Для детальной истории создания
 см. Куинна. И до сих пор, по определению, килограмм — это масса
небольшого металлического цилиндра, лежащего в сейфе Международного бюро
мер и весов недалеко от Парижа (хотя технически он находится не на
территории Франции). Он лежит в сейфе, который открывается тремя
ключами, под тремя стеклянными куполами, — небольшой платино-иридиевый
цилиндр, который определяет, что такое килограмм. Чтобы сориентировать
вас в географии, вот карта Парижа с нынешним эталоном килограмма (на
юго-западе), наш оригинал (на северо-востоке), — оба в желтой рамке, — и
некоторые другие достопримечательности Парижа:
см. Куинна. И до сих пор, по определению, килограмм — это масса
небольшого металлического цилиндра, лежащего в сейфе Международного бюро
мер и весов недалеко от Парижа (хотя технически он находится не на
территории Франции). Он лежит в сейфе, который открывается тремя
ключами, под тремя стеклянными куполами, — небольшой платино-иридиевый
цилиндр, который определяет, что такое килограмм. Чтобы сориентировать
вас в географии, вот карта Парижа с нынешним эталоном килограмма (на
юго-западе), наш оригинал (на северо-востоке), — оба в желтой рамке, — и
некоторые другие достопримечательности Парижа: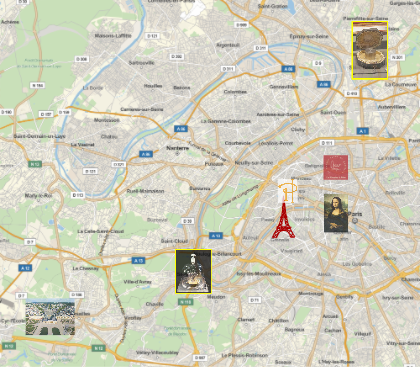
К этому эталону килограмма, который сделал меня несчастным, очень сложно получить доступ. Каждые несколько лет небольшая группа людей заново измеряет его вес (массу). И, конечно, результат, согласно определению и договору, заключенному на первой Генеральной конференции по мерам и весам в 1889 году, оказывается равен одному килограмму.
Спустя годы первый эталон килограмма получил десятки братьев и сестер в виде национальных эталонов других стран (одинакового размера, материала и веса с точностью до нескольких микрограммов, которые тщательно регистрируются). Жаль, что интернет не был изобретен раньше, потому что в таком случае у меня был бы канал связи, чтобы сказать, что случилось с похищенным аргентинским эталоном 45; после этого он был переплавлен. Сразу же после создания они имели один и тот же размер и вес. Можно было предположить, что вес этих цилиндров будет стабилен. Однако история рассудила иначе. Повторные измерения показали, что практически все эталоны становились с каждым годом все тяжелее. Или, что более вероятно, это международный прототип становился все более легким.
За многими из этих сравнений я с большим интересом наблюдал у себя с неба. Сравнение их масс представляло значительные трудности. Во-первых, сначала необходимо доставить национальные прототипы в Париж. Я молча слушал продолжительные дискуссии с членами TSA, когда пришел метролог с платиновым килограммом, материалы для которого стоят около 50000$ (нужно добавить еще 20000$ на изготовление), который лежал в блестящем золотистом контейнере и который должен открываться только в чистой комнате в перчатках и с капой во рту, и чтобы его никогда не касалась человеческая рука), и объяснил все это членам TSA (официальное письмо оказывается в таком случае большим подспорьем). То, что я наблюдал здесь, было даже смешнее, чем сцены из фильма 1001 грамм.
Затем наступает сложная процедура очистки горячей водой, спиртом и УФ-излучением. Все образцы теряют вес в этом процессе. Затем все они тщательно сравниваются друг с другом. И в результате все это с высокой степенью вероятности приводит к тому, что мой любимый международный эталон килограмма теряет вес. Этот факт лишает меня сна.
Вот результаты третьей верификации (с 1988 по 1992). На рисунке показана разница в весе по сравнению с международным прототипом:

Чтобы узнать об измерениях, проведенных за последние два года, см. эту статью.
Говоря, что килограмм «теряет вес», я имею в виду следующее. По определению (не зависящему от его «реальной объективной» массы) международный эталон имеет массу ровно 1 кг. По сравнению с этой массой большая часть других эталонов килограмма, кажется, набирает вес. Так как другие эталоны создавались постепенно на протяжении более чем 100 лет с использованием различных методов, весьма вероятно, что международный эталон становится легче со временем (это происходит не из-за жадности Чаушеску, крадущего платину; румынский прототип уже в 1889 году был на 953 мкг легче, чем международный эталон килограмма).
Уиллард Гиббс, мой старый друг, часто говорит о том, что в его родной стране до сих пор используется фунт, а не килограмм. Его голос на выборах в этом году явно будет за Берни. По крайней мере, фунт составляет определенную долю килограмма, поэтому все, что будет происходить с килограммом, повлияет таким же образом и на фунт:
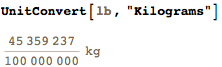
Новая СИ
Но вскоре все мои мечты и многовековые надежды сбудутся, и я снова смогу уснуть. В 2018 году, то есть всего через два года, произойдут самые грандиозные (начиная с моей работы с Лапласом) изменения в истории единиц и измерений.
Все единицы измерения будут основаны на вещах, доступных всем и везде (имеется в виду доступ к некоторым современным физическим приборам и устройствам).
Внизу, на Земле их начали называть "референтные константы".
Некоторые люди также называют новую СИ «квантовой СИ» из-за ее зависимости от постоянной Планка и элементарного заряда е. В дополнение к важности постоянной Планка (h), с h и e в квантовой механике связаны следующие квантовые эффекты: эффект Джозефсона и связанная с ним постоянная Джозефсона Kj = 2е/h, а также квантовый эффект Холла с константой Клитцинг RK = h/е2. Квантовый метрологический треугольник: подключение частоты и электрического тока посредством туннелирования одиночных электронов, соединение частоты и напряжения через эффект Джозефсона и подключение напряжения и электрического тока через квантовый эффект Холла станет прекрасной реализацией электрических величин (через много-много лет, так отметил Пенин, нам придется беспокоиться об эффектах QED второго порядка, но это будет еще не скоро).
У BIMP уже есть новый логотип для будущей Международной системы единиц:

Если конкретно, то предложение таково:
- Секунда по-прежнему будет определяться через микроволновое излучение атома цезия.
- Метр будет по-прежнему определяться через точно определенную скорость света.
- Килограмм будет определяться через точное значение постоянной Планка.
- Ампер будет определяться через точно определенную величину элементарного заряда.
- Кельвин будет определяться через точно определенное значение постоянной Больцмана.
- Моль будет определяться через точное (вычисляемое) значение.
- Кандела будет определяться посредством точного значения отношения кандела стерадиан-на-ватт при фиксированной частоте (уже сейчас используется в отдельных случаях).
Я настоятельно рекомендую вам прочитать брошюру проекта новой СИ. Мы с Лапласом много обсуждали ее, и она нам понравилась. Вот облако слов из новой брошюры СИ:

Пока не забыл: ниже приведены некоторые комментарии в отношении других единиц.
Секунда
Я до сих пор помню, когда мы обсуждали введение метрического времени в 1790-е годы: 10-ти часовой день, 100 минут в часе и 100 секунд в минуте. Оглядываясь назад, я понимаю, что это была не такая уж и хорошая идея. Привычки людей иногда слишком трудно изменить. И я так рад, что за последние годы смог заинтересовать Альберта Эйнштейна метрологией. Мы много беседовали о значении времени и о разнице между измеряемым местным и координатным временем. Но об этом мы поговорим не сегодня. Неопределенность секунды на сегодняшний день меньше, чем 10-16. Может быть, в один прекрасный день цезий заменят алюминием или другим элементом, чтобы уменьшить неопределенность в 100 или даже в 1000 раз. Но это не меняет дух нового СИ; речь идет о небольших технических изменениях (если интересуют подробности, см. эту статью).
Очевидно, что сегодняшнее определение секунды гораздо лучше предыдущего. В то время, когда цены на фондовом рынке сопоставляются на уровне микросекунд, изменение продолжительности дня из-за землетрясений, таяния ледников, дрейфа континентов и других явлений, происходящих на протяжении более ста лет, оказывается довольно большим:

Моль
Я слышал, что некоторые химики жалуются, что моль (их любимая единица, введенная в СИ только в 1971 году) будет опошлен. В используемой в настоящее время СИ моль определяется через количество атомов в углероде-12. В новой СИ речь будет идти просто о подсчете объектов — истинный химический эквивалент чертовой дюжины. Основанный на числе Авогадро, моль играет важную роль в соединении микромира с макромиром. Более приземленное определение моля зависит от данного количественного значения — например, от значения рН. Секунда — базовая единица времени в СИ; моль — базовая единица физической величины или количества вещества:

Однако термин "количество вещества" нравится далеко не всем. Даже в этом году (2016) были предложены альтернативные названия: например, стехиометрическое количество. В течение последних десятилетий было предложено заменить все разнообразие названий на формулировку «количество вещества». Вот некоторые примеры:

Но в СИ определяется только название единицы измерения — «моль». Именование физической величины, которая измеряется в молях, остается Международному союзу теоретической и прикладной химии.
Чтобы посмотреть последние обсуждения этого года, см. статьи Леонарда: "Почему «количество вещества» так плохо понято? Всему виной таинственный Авогадро!".
А что, если бы мы могли бы создать «идеальный куб», который представлял бы число Авогадро? Это было бы легко концептуализировать. Такой вариант и был предложен несколько лет назад — вариант, совместимый со значением постоянной Авогадро (в результате получился бы куб с длиной кромки из 84 446 888 элементов). Во время игры в небесный крикет я спросил Сриниваса Рамануджана и Харольда Харди, его давнего друга, о том, что особенного в числе 84 446 888, но пока что они не придумали ничего глубокого. Он сказал, что 84446888 = 23 * 17 * 620933, и число 620 933 появляется, начиная с позиции 1 031 622 десятичных знаков числа π, но я лично не вижу в этом чего-либо, связанного с метрологией.
Вот последнее значение CODATA (Комитет по данным для науки и техники) из списка констант, единиц измерения и неопределенностей Национального института стандартов и технологий:

Вышеупомянутый куб оказывается слишком мал.

Интересно, что если бы мы согласились на вариант объемно центрированной решетки с одним дополнительным атомом в элементарной ячейке, то мы могли бы по-прежнему придерживаться интерпретации куба:

А гранецентрированная решетка не будет работать:

Но алмазная (кремниевая) решетка будет:

Обобщим:

Вот еще одна мелочь:
В самый разгар холодной войны принятое значение числа Авогадро изменилось в третьем знаке. Это было серьезное изменение, учитывая, что в настоящее время ведется затяжной спор относительно разногласий в отношении шестого разряда. Можете ли вы объяснить внезапное уменьшение числа Авогадро во время холодной войны?
Знаете ответ? Если нет, смотрите здесь или здесь.
Однако я ушел в сторону от основной мысли. Так как меня больше интересуют единицы измерения механических величин, я предоставлю моему старому другу Антуану Лавуазье судить о новом определении моля, так как именно он был химиком в нашей команде.
Кельвин
Уиллард Гиббс убедил меня в том, что температура должна определяться механически. Я до сих пор пытаюсь понять, что думает об этом Джон фон Нейман (так как я никогда в полной мере не понимал его вечерние лекции о факторах типа II и типа III, мое мнение о кельвине так и не сложилось). Различные температуры соответствуют неэквивалентным представлениям алгебр. Я не думал о том, как лучше определить кельвин с точки зрения алгебраической квантовой теории поля. Я спросил Джона о его мнении касательно первопринципной оценки h/k, основанной на теории Томита-Такесаки, и даже он не был уверен в этом. Он рассказал мне кое-что о тепловом времени и температуре алмаза, но я не много из этого понял.
И дальше у нас есть возможность получения значения константы Больцмана. Даже через 40 лет после публикации статьи Коппе-Хубера неясно, возможно ли это. Я уже размышлял об этом, и я принимаю во внимание различные варианты. Как я уже говорил, мне неясно, как определить значение температуры и единицы ее измерения. Не сомневаюсь, что новое определение кельвина будет большим шагом вперед; только вот последним ли?
Ампер
Это одно из самых прямых, интуитивных и красивых определений в новой СИ: ток — это просто определенное число текущих электронов (в секунду). Определение значения ампера через число элементарных зарядов просто гениально. Когда оно впервые было предложено, Роберт Милликен был так счастлив, что пригласил многих из нас встретиться во второй половине дня во дворе своего дома. Как в теории, так и на практике, измеряя электрический ток электронов в кристаллических объектах, мы должны помнить о том, что электроны являются квазичастицами. Однако с 1959 года благодаря Вальтеру Кону мы знаем, что не стоит ожидать, что заряд электрона в кристалле будет таким же, как заряд голого электрона. Так как элементарный заряд — это заряд довольно небольшой, то вопрос измерения дробных зарядов сейчас не актуален. Лично я считаю, что вклад Роберта в определение физических констант в начале 20-го века явно недооценен (Роберт Эндрюс всегда знал, что делал).
Кандела
Заслуживает ли эта единица быть в числе основных? Вся история человекоцентрированных физиологических единиц довольно запутанна. Очевидно, что они чрезвычайно полезны. Мы все видим и слышим каждый день, каждую секунду. Но что, если человеческая раса продолжит развиваться (в контексте идей Дарвина)? Как это будет соответствовать нашей мантре «на все время»? У меня кое-какие мысли на этот счет, но выкладывать их здесь и сейчас значило бы уводить повествование от главной для обсуждения темы.
Почему основных единиц измерения именно 7?
Хочу отметить, что сначала я был очень обеспокоен введением некоторых дополнительных единиц измерения, используемых сегодня. В процессе бесконечных дискуссий Гауссу (моему партнеру по шахматам) удалось убедить меня, что мы можем свести все измерения электрических величин к измерению механических свойств, так что я в итоге стал неплохо разбираться в системе СГС, которая сначала мне не понравилась. Однако система единиц измерения, созданная человеком, должна быть как можно более полезной, и, если уж эти семь единиц выполняют свои функции лучше всех, то их и должно быть семь. В принципе можно даже исключить единицу измерения массы и выразить массу через время и длину. Однако, кроме того, что это непрактично, я уверен, что этот подход концептуально неправильный. Недавно я обсуждал этот вопрос с Карлом Фридрихом. Он сказал, что в конце 1820-х гг. была идея просто использовать время и длину, но от этого подхода в дальнейшем отказались. При жизни Гаусс не имел возможности обсудить с Кантом понятие массы, зато за последнее столетие они договорились о массе как априори (по крайней мере в этой вселенной).
Девизом для оригинальной метрической системы стала фраза: «для всех людей, на все времена». Текущая СИ уже реализует первую часть девиза — «для всех людей», а с учетом грядущих изменений и вторая его часть вскоре станет реальностью. Вы не можете себе представить, что это значит для меня. Кажется, фундаментальные константы максимально могут изменяться на величину, равную порядка 10-18 в год. Это на много порядков дальше от доступной в настоящее время для большинства единиц точности.
Конечно, в новой СИ некоторые значения будут более громоздкими. Если мы будем рассматривать текущие значения CODATA как точные, то, например, константа фон Клитцинг е2/h получится довольно объемной:
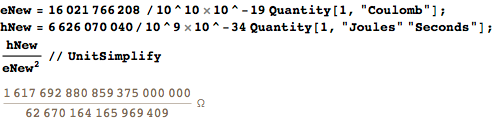
Целая часть последнего результата составляет, конечно, 25,812Ω. Однако что это — периодическая десятичная дробь или конечная? Простые множители знаменателя говорят нам о периодичности:

Прогресс — это хорошо, но, как это часто бывает, у него тоже есть своя цена. В то время как новые определения единиц СИ красивы, понять их становится сложнее, и учителя физики и химии должны будут придумать способы объяснения этих новых определений ученикам (чтобы узнать о первых попытках, см. эту и эту статьи).
А сколько раз я встречал учебники, в которых величина магнитной проницаемости (проницаемость вакуума) μ0 равнялась 4π10-7N/A2? Магнитные и электрические константы станут в новой СИ измеряемыми величинами. Текущее точное значение:

С учетом постоянной Планка h и элементарного заряда е величина μ0 понесет неопределенность константы тонкой структуры α. К счастью, безразмерная константа тонкой структуры α является одной из самых известных констант:

Ну и что? Издательства учебной литературы не возражают против такого повода для переиздания всех своих книг. Это вообще прекрасный повод продать больше новых книг.
С учетом того, что μ0 в будущем станет измеряемой величиной, я предсказываю гораздо большее использование аутсайдера среди фундаментальных констант — волнового сопротивления вакуума Z — в будущем:

Я аплодирую всем физикам и метрологам за ту тяжелую работу, которую они осуществляли в течение последних 225 лет, венцом которых стали новые определения, основанные на физических константах. Так что, мои дорогие первые члены комитета, эти определения красивы и вечны.
Я знаю, что это немного нескромно, но Жозеф Луи Лагранж сказал мне, что он сожалеет о том, что мы не представили основные и производные единицы еще в 1790-х годах. Сейчас, когда постоянная Планка очень важна для новой СИ, он думает, что у нас должна была быть именная основная единица измерения для действия. А еще, что нужно затем сделать массу производной величиной. Несмотря на то, что это могло бы стать высшим пилотажем классической механики, он все же понимает, что единица измерения для действия не стала бы популярной среди фермеров и крестьян в качестве каждодневной единицы измерения.
У меня нет времени вдаваться в подробное обсуждение ежеквартальных фестивалей в саду, которые устраивает Бриджмен. Я стараюсь участвовать в каждом из них, если позволяет график. Такие мероприятия заставляют прислушиваться к общей дискуссии о преимуществах и недостатках альтернативных систем единиц измерения. Как и ожидалось, Юлиус Валлот, Ян де Бур, Эдвард Гуггенхайм, Вильям Страуд, Джованни Джорджи, Отто Гёльдер, Рудольф Флейшманн, Ульрих Штилле, Хасслер Уитни и Честер Пэйдж оказались наиболее разговорчивы на этих вечеринках. Дискуссия о согласованности и полноте системы единиц измерения и о том, что такое физическая величина, продолжаются дальше. Недавно обсуждение того, является ли вероятность физической величиной продолжалась в течение шести часов, и в итоге решение так и не было найдено. Я предложил в следующий раз пригласить Ричарда фон Мизеса и Рейхенбаха — они точно предложили бы что-то стоящее. Отто всегда жалуется на вечеринках, что математиков больше не интересует, как раньше, тема единиц измерения и систем единиц измерения, и что он очень счастлив видеть, что в последнее время физики-теоретики время от времени поднимают эту тему: см. векторную дифференциацию физических единиц или недавнюю статью об общей структуре систем единиц измерения. И когда он увидел в статье о разбирательствах в Дагштуле, что теория нового типа объединяет единицы измерения и физические величины, он был чрезвычайно взволнован.
Интересно отметить, что примерно такие же дискуссии проходили три года назад (и с тех пор регулярно организуются) во время ежемесячных горных прогулок, организуемых Клодом Шенноном. Силард утверждает, что «бит» должен стать основной единицей СИ в будущем. По его мнению, информация как физическая величина сильно недооценена.
Повторюсь опять: новая СИ будет просто замечательна! Однако я хотел бы изменить несколько деталей. Вот текущий статус радианов и стерадианов, которые в SP 811 определяются как производные единицы: «Радиан и стерадиан — специальные названия для одного, которые могут использоваться для передачи информации о количестве». Однако не могу не отметить, что эксперты обсуждают эту тему в деталях.
В честь новой СИ мы провели сбор средств, чтобы отпраздновать это событие. Мы собрали достаточно, чтобы нанять Микеланджело. Он будет делать скульптуру. Эскизы, представленные Комитету (мне повезло иметь почетное председательство) интригуют. Я уверен, что она составит конкуренцию самому Давиду. Каждый человек в один прекрасный день сможет увидеть ее (это зависит от вашего текущего возраста и вредных привычек). Помимо собственно констант и единиц он планирует также создать скульптуры Планка, Больцмана и Авогадро, так как в честь них названы константы. И если Макс мог позировать сразу, то с тем, чтобы получить разрешение на то, чтобы Больцман покинул на время ад, возникли проблемы (Милликен и Флетчер были, по понятным причинам, немного разочарованы). Как ни странно, именно Поль Адриен Морис Дирак придумал, как убедить Люцифера, чтобы тот отпустил Больцмана. Ирония в том, что сам Поль не был так увлечен новой СИ из-за того, что константы сами зависели от времени на протяжении миллиардов лет. В любом случае, Поль отметил, что три фундаментальные константы: постоянная Планка (6,62… ×10 34 Дж · с), число Авогадро (6,02… × 1023 /моль), и гравитационная постоянная (6,6… × 10-11 м3/(кг · с)) все начинаются с цифры 6. Тот факт, что все три фундаментальные константы образуют число зверя, произвел впечатление на Люцифера, так что можно ожидать, что он одобрит временный отпуск для Людвига.
Как бывший моряк, я также указал Люциферу, что средняя глубина океана составляет ровно 66% от его высоты (2443 м, в соответствии с подробным повторным анализом Божественной комедии Данте). Ему так полюбился этот милый факт, что теперь он мне должен.

До сих пор Люцифер настаивает на комбинации G(mе / (hк))1/2 для скульптуры. Причина очевидна:

Посмотрим, как будет разворачиваться дискуссия. В этой комбинации на самом деле нет ничего плохого (пускай даже она физически не имеет смысла), так что мы могли бы согласиться с его требованиями.
Также уже была достигнута договоренность о музыке: мы будем играть Sinfonia de motu Войцеха Киляра, который представил физические константы в виде музыкальной композиции, используя только ноты C, G, E, H (си-бемоль в англоязычных странах), и А (которая представляет атом цезия). И мы хотим убедить Рильке в честь этого события написать стихи.
Внизу, на Земле, появление основанных на константах единиц измерения также будет отмечаться. Я с нетерпением жду документального кино Статус единицы измерения об истории килограмма и его переопределение через постоянную Планка.
Путь к изменению определения килограмма
Я уже упоминал, что важнейшим нововведением новой СИ будет измененное определение килограмма. В конце концов, килограмм, наличествующий в текущем варианте СИ, — это артефакт. Вдобавок многие другие производные единицы зависят от него: скажем, вольт. Изменение определения килограмма сделает счастливыми многих электриков.

Результирующее значение для константы Клитцинг и константы Джозефсона очень близко к последнему значению CODATA постоянной Планка:

Килограмм является основной единицей СИ для количества массы. Масса наиболее актуальна для механики. Благодаря второму закону Ньютона
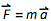 масса тесно связана с силой. Предположим, что мы поняли длину и время (а значит, и ускорение). Что дальше? Уильям Фрэнсис Мэджи писал в 1912 году:
масса тесно связана с силой. Предположим, что мы поняли длину и время (а значит, и ускорение). Что дальше? Уильям Фрэнсис Мэджи писал в 1912 году:Было бы неуместно догматизировать, и я, соответственно, должен жаждать прощения за то, что часто выражаю свое мнение, полагая, что менее предосудительно быть эгоистичным, нежели догматичным… Первый вопрос, который я буду рассматривать, поднимается сторонниками динамического определения силы и заключается в том, в каком порядке появляются идеи понятий силы и массы; другими словами, какое из понятий является первичным… Он [Ньютон] предлагает массу в качестве фундаментальной величины, которая необходима для установления динамического измерения силы… Я не могу найти у Лагранжа какого-нибудь определения массы… Для того, чтобы измерить массу, мы должны начать с интуитивного знания о силе, а затем использовать его в экспериментах, с помощью которых мы сначала определяем, а затем измеряем массу… Теперь, благодаря постоянству массы материи, стало удобно строить нашу систему единиц с массой в качестве одной из основных единиц.
Анри Пуанкаре в своей книге Наука и Метод пишет:
Зная силу, легко определить массу; на этот раз определение должно быть заимствовано из динамики; нет никакого способа делать это иначе, так как в результате мы должны получить представление о различии между массой и весом. Здесь, опять же, к определению должны подводить эксперименты.
У меня всегда было интуитивное понимание значения массы в механике, хотя вплоть до середины двадцатого века я никогда не был в состоянии выразить его четко. Только недавно, с помощью Валентина Бергмана и Жана-Мари Сурио я вполне понял роль массы в механике: масса — это элемент второй когомологической группы алгебры Ли группы Галилея.
Масса как физическая величина проявляется в различных областях физики. В классической механике она связана с динамикой, в общей теории относительности — с искривлением пространства, а в квантовой теории поля масса появляется в качестве одного из операторов Казимира группы Пуанкаре.
В нашем еженедельном семинаре «Философия физики», который в этом году был возглавлен Иммануэлем, Хансом Рейхенбахом и Карлом Фридрихом фон Вайцзеккером (именно Паскуаль Йордан предложил, чтобы семинар вели трое мужчин), мы в течение 5 встреч обсуждали природу массы. Темами для семинаров этого года стали правила суперселекции массы в нерелятивистской и релятивистской теориях, концепции и использование отрицательной массы, неопределенность отношений массы-времени, не-Хиггсовские механизмы производства и масштабирования массы в биологии и спорте. Мне нужно по крайней мере три дня подготовки к каждому из семинаров, а список рекомендуемых для чтения книг составляет более девяти страниц (что подчеркивает, как много существует явлений конденсированных сред). Я с нетерпением жду этого года, посвященного массе; и я уверен, что пойму многое. Я надеюсь, что Эренфест, Паули и Ландау не будут постоянно прерывать ораторов, как они это делали в прошлом году (беседа о массе в общей теории относительности была особенно неудачной в этом смысле). В последнем семинаре этой серии я должен буду произнести речь. Что касается законов масштабирования, мой любимый пример выглядит следующим образом:

Я также собираюсь рассказать о недавно найденном степенном законе хищника-жертвы.
Что касается спорта, у меня уже есть хороший пример, на который меня вдохновили Тексье и др.: соотношение между массой спортивного мяча и его максимальной скоростью. Следующая диаграмма позволяет мне предположить, что speedmax ~ ln(mass). Двигайте мышью, чтобы посмотреть массу мяча и максимальную скорость (в приложенном документе)::

Для семинара по отрицательным массам у нас были некоторые интересные домашние задания: визуализиция траектории классической точечной частицы со сложной массой (двухъямный потенциал). Так как я видел некоторые из работ Бендера по траекториям комплексной энергии, те траектории, которые я получил для комплексных масс, меня не удивили:
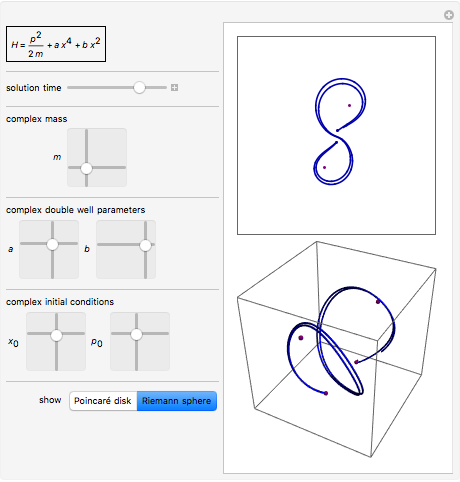
Последние замечания.
Новое определение целиком звучит так:
килограмм является единицей массы; его величина устанавливается путем фиксации численного значения постоянной Планка, равной точно 6.62606X * 10-34, когда она выражается в единицах s-1 · m2 · kg, эквивалентным J · s. Здесь X обозначает некоторых цифры, представляющие собой последние экспериментальные значения.
А килограммовый цилиндр может окончательно уйти в отставку как самый драгоценный артефакт в мире. Я ожидаю, что вскоре после этого события международный эталон килограмма окажется, наконец, в Лувре. Как только Лувр был объявлен "местом для объединения памятников всех наук и искусств" в мае 1791 года, а затем в 1793 году был открыт, все члены комитета согласились с тем, что в один прекрасный день, когда первоначальный эталон килограмма будет заменен на что-то другое, он перейдет в Лувр. Этот эталон заслужил свое место. Я даже ставлю на то, что в течение нескольких лет отставной эталон под тремя стеклянными куполами станет одним из самых популярных объектов Лувра. И та очередь, которая образуется перед ним из физиков, химиков, математиков, инженеров и метрологов, будет длиннее очереди на Джоконду. Я хотел бы также сделать ставку на то, что красивые миниатюрные реплики килограмма в течение нескольких лет станут самым продаваемым товаром в магазине при Лувре:

В то же время, может быть, стоит оставить эталон там, где он сейчас находится, еще на 50 лет, чтобы измерять его и сравнивать с эталоном, изготовленным на основе точного значения постоянной Планка. Тогда мы, наконец, узнаем наверняка, действительно ли международный прототип килограмма терял вес.
Позвольте мне быстро повторить все те шаги, которые привели нас к новому, "электронному" килограмму.
Можно было бы определить килограмм через число Авогадро как определенное число атомов, скажем, 12С. Но из-за энергии связи и поверхностных эффектов, происходящих в углероде (алмаз или графен), составленном из n = round(1 кг / m(12С)) атомов так, чтобы получилась масса в 1 килограмм, все n атомов углерода-12 должны быть хорошо разделены. В противном случае мы получили бы дефект массы (вспомните знаменитую формулу Альберта E = mc2), а масса эквивалента одного килограмма или массива углерода по сравнению с тем же числом отдельных, хорошо разделенных атомов составила бы порядка 10-10. Используя энергию углерод-углеродной связи, оценим разности масс:

Разница масс при таком размере и весе в 1 кг может быть легко обнаружена с помощью современного масс-компаратора.
Чтобы передать масштаб: это было бы эквивалентно релятивистскому преобразованию массы (эйнштейновской) от расхода энергии на то, чтобы фехтовать целый день:

Это не означает, что нельзя определить килограмм через массу атома или его часть. Учитывая, что масса атома углерода равна m(12C), атомная единица массы u = m(12C)/12; следовательно, с помощью u можно легко перейти к постоянной Планка:

Я с большим интересом прочитал последнее сравнение использования различных наборов констант для определения килограмма. Конечно, если масса атома углерода-12 будет иметь определенное значение, то постоянная Планка станет измеряемой. Мне кажется, что эстетически более предпочтительно иметь точное значение постоянной Планка.
Я внимательно следил за тем, что делалось в последнее десятилетие для переопределения килограмма. События последних 20 лет позволяют предположить, что килограмм скоро упадет с пьедестала.
И когда 11 лет назад я прочитал статью Яна Миллса, Питера Мора, Терри Куинна, Барри Тейлора и Эдвина Уильямса под названием "Переопределение килограмма: решение, время которого пришло" в Metrologia (этот журнал находится в моем списке фаворитов на втором месте после ежедневного Новые поступления, совместно издаваемого Hells 'Press, издательской группой Heaven, Jannah Media и Deva University Press), я уже знал, что скоро мои мечты сбудутся. В тот момент, когда я прочитал Приложение А.1 Определения, которые фиксируют значение постоянной Планка h, я знал, что будет дальше. Хотя сама идея витала в воздухе гораздо дольше, теперь она оформилась в настоящую программу, которая будет реализована в течение десяти лет.
Джеймс Клерк Максвелл писал в своем Трактате об электричестве и магнетизме 1873 г.:
При выработке универсальной системы единиц мы можем вывести единицу массы из уже определенных длины и времени, и, учитывая современное состояние науки, мы можем сделать это лишь в грубом приближении; если же мы рассчитываем на то, что в ближайшее время будем в состоянии определить массу одной молекулы стандартного вещества, мы можем подождать этого определения до фиксации универсального стандарта массы.
Примерно до 2005 года Джеймс Клерк считал, что масса должна определяться через массу атома, однако затем он изменил свое мнение и в настоящее время выступает за определение на основе постоянной Планка.
В беседе с Альбертом Эйнштейном и Максом Планком (кажется, это было в начале семидесятых) в кофейне в венском стиле (Макс любит торт Захер и был счастлив, когда Франц и Эдуард Захеры открыли свой ныне знаменитый HHS («Небесный отель Захер „)), Альберт предложил использовать два свои знаменитые уравнения: E = mc2 и E = hf для поиска m, чтобы получить m = hf / с2. Таким образом, если мы определим h, как это было сделано с с, то мы узнаем m (Комптон утверждал, что это просто его уравнение переписали, а Нильс Бор заметил, что мы не можем доверять E = mc2 из-за его относительно слабой возможности экспериментальной проверки, но я думаю, что он просто издевается над Эйнштейном — мстит за какую-нибудь Сольвеевскую конференцию, посвященную обсуждению мысленных экспериментов. И, конечно же, Бор не мог сопротивляться Δm Δt ~ h/с2 как причине того, почему мы не можем определять секунду и килограмм независимо друг от друга, так как ошибка в одном предполагает ошибку в другом для любого конечного времени измерения массы. Но Розенфельд убедил Бора, что до этого еще далеко, так как точность измерения массы составляет около 10-52 кг для массы m в 1 кг.).
Частотный эквивалент, соответствующий f = mс2/h, не практичен для килограмма массы, так как это будет означать, что f~1,35×1050 Гц, а это слишком велико для любого эксперимента. Однако эксперименты, проведенные в Беркли в последние годы, возможно, позволят использовать такие методы в микроскопическом масштабе. На протяжении более чем 25 лет на каждом заседании НФС (небесного физического общества) Луи де Бройль настаивает на том, что эти частоты являются реальными физическими процессами, а не только удобными математическими инструментами.
Таким образом, мы должны знать значение постоянной Планка h. До сих пор килограмм определяется как масса его эталона. В результате мы можем измерить величину h с помощью текущего определения килограмма. После того, как мы узнаем значение h с точностью примерно до 10-8, мы сможем определять конкретное значение h. С того момента килограмм станет неявно определяться через значение постоянной Планка. При переходе эти два определения будут перекрываться в своей неопределенности, и никаких разрывов для любых производных величин не возникнет. Международный прототип за последние 100 лет потерял порядка 50μг веса (относительное изменение 5×10-8), поэтому значение постоянной Планка с погрешностью менее 2×10-8 гарантирует, что масса объектов существенно не изменится.
За последние 116 лет значение постоянной Планка стало точнее на 7 цифр. Настоящий успех! В своей статье "О законе распределения энергии в нормальном спектре» Макс Планк впервые использовал символ h, и впервые — численное значение постоянной Планка (в статье, опубликованной несколько месяцев назад, Макс использовал символ b вместо h):

Я спросил Макса, почему он выбрал символ h, и он ответил, что не помнит. Во всяком случае, он сказал, что это был естественный выбор (как и в случае с символом к для постоянной Больцмана). Иногда можно прочесть, что символ h использовался, чтобы выразить немецкое слово Hilfsgrösse (вспомогательная переменная); Макс сказал, что, возможно, так и было, и что он действительно не помнит.
В 1919 году Реймонд Тайер Бирге опубликовал первое детальное сравнение различных измерений постоянной Планка:

Значение постоянной Планка изменилось с 6,55×10-34 J · s до значения 2016 года 6,626070073(94)×10-34 J · s: удивительный прогресс.
Следующая интерактивная демонстрация позволяет увеличивать и уменьшать масштаб, чтобы увидеть прогресс в измерении постоянной Планка h в течение последнего столетия. Наведите курсор мыши на кривые Белла (демонстрирующие неопределенность значений) в документе, чтобы увидеть эксперимент (для детального обсуждения многих экспериментов по определению h см. эту статью):
Моя группа охотно следила с небес за двумя важными экспериментами последних лет: экспериментом ватт-баланса и проектом Авогадро. Как человек, который при жизни занимался механическими измерениями, я лично люблю эксперимент ватт-баланса. Построение механического устройства, которое, благодаря хитрому трюку от Брайана устраняет неизвестную геометрическую величину, достойно аплодисментов. Особенно порадовала недавняя домашняя версия LEGO «сделай сам». При вложении нескольких сотен долларов каждый может измерить постоянную Планка у себя дома! Мир очень изменился с тех пор, как я жил в нем. Вы можете даже проверить вашу карту памяти до того, как вы поместите туда файл, и после, чтобы посмотреть, изменилась ли его масса.
Но мой дорогой друг Лавуазье, что ожидаемо, всегда любил проект Авогадро, призванный определить значение постоянной Авогадро с высокой точностью. Чистый кремний (99,995%) заставляет сердце химика биться чаще. Произведение числа Авогадро с постоянной Планка NАh связано с постоянной Ридберга. К счастью, как мы видели выше, постоянная Ридберга определена с точностью около 11 цифр; это означает, что NАh позволяет найти значение нашей любимой постоянной Планка h с высокой степенью точности. Еще во время моей жизни люди начали понимать природу химических элементов. Мы еще ничего не знали об изотопах; если бы вы сказали мне, что существует более чем 20 изотопов кремния, я бы даже не понял вашего утверждения:

Я поражен тем, что сегодня человечество может классифицировать отдельные атомы по количеству нейтронов. Кремниевые сферы проекта Авогадро состоят на 99,995% из кремния 28:
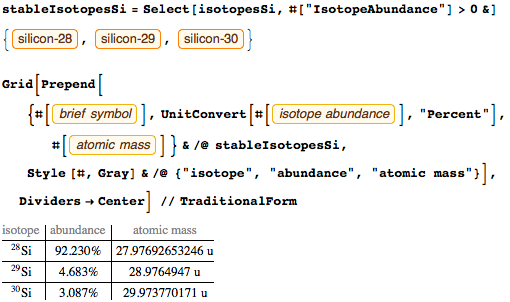
Пока компараторы массы достигают точности уровня 10-11, они способны только сравнивать массы, а не определять их. Массу можно будет определить после того, как постоянная Планка получит фиксированное значение с помощью ватт-баланса.
Я считаю, что постоянная Планка является одной из самых захватывающих констант. Однако она царит в микромире, и потому и едва заметна в макроскопических масштабах.
Несколько лет назад я очень расстраивался из-за того, что, как мне казалось, наша мечта о создании определений для единиц никогда не будет реализована. Я потерял сон, когда значения для постоянной Планка из опытов с ватт-балансом и экспериментов c кремниевой сферой Авогадро были совсем разными. Поэтому каким облегчением для меня было видеть, что за последние несколько лет все расхождения были преодолены! А теперь рабочая масса снова синхронизирована с международным прототипом.
Перед тем как закончить, позвольте мне сказать несколько слов о постоянной Планка. Постоянная Планка — архетипическая величина; можно было ожидать, что она появится в квантово-механических явлениях. И когда постоянная Планка стремится к нулю, мы возвращаемся к классической механике (в сингулярном пределе). Я думал так до недавнего времени. Так как я хожу на еженедельные лекции Владимира Арнольда, которые он стал давать летом 2010 года после того, как присоединился к нам, у меня появились серьезные оговорки в отношении таких упрощенных взглядов. В своей лекции о многомерной геометрии он рассматривал симплектического верблюда; с тех пор я рассматриваю соотношение неопределенностей Гейзенберга скорее как классический реликт, чем квантовое свойство. А с тех пор, как Вернер Гейзенберг показал мне статью Бродского-Хойер о распространении ħ, у меня появился гораздо более сдержанный взгляд на куб BZO (Бронштейн-Зельманов-Окунь). И давайте не будем забывать про недавние попытки выразить квантовую механику вообще без обращения к постоянной Планка. Несмотря на то, что мы многое понимаем в постоянной Планка и ее очевидных проявлениях (таких, как «коэффициент преобразования» между частотой и энергией фотонов в вакууме), я думаю, что самые глубокие ее тайны до сих пор не обнаружены. Чтобы разгадать их, нам потребуется длинная поездка на симплектическом верблюде по пустыням гипотетических мультиверсумов. И Поль Дирак считает, что роль постоянной Планка в классической механике еще недостаточно хорошо изучена.
Долгое время сам Макс считал, что в фазовом пространстве (классическом или через преобразование Вигнера) минимальный объем будет составлять порядка его постоянной h. Как один из отцов квантовой механики, Макс до сих пор следует концептуальным разработкам, — особенно программе декогеренции. Он был поражен, когда 15 лет назад были обнаружены субпланковские структуры. Юджин Вигнер сказал мне, что он предполагал наличие таких тонких структур уже начиная с конца 1930-х годов. С тех пор он любил играть с построениями функции Вигнера для всех видов гипергеометрических потенциалов и квантовых ковров. Его любимой до сих пор остается функция Вигнера осциллятора Дуффинга. Однако высокоточное решение нестационарных уравнений Шредингера, следующее из построения функции Вигнера на основе дробного преобразования Фурье, может быть найдено быстрее. Вот как начальный волновой пакет в форме кривой Гаусса выглядит после трех периодов внешней силы. Синий прямоугольник представляет собой площадь плоскости хр площади h:

Вот некоторые увеличенные изображения (окрашены в соответствии со знаком функции) последней функции Вигнера. Каждый квадрат имеет площадь 4h и демонстрирует различные субпланковские структуры:

Предстоящее определение килограмма через постоянную Планка — серьезное интеллектуальное и технологическое достижение человечества. За ним стоят два столетия упорного труда в метрологических институтах. Это событие закладывает некоторые глубочайшие физические истины, обнаруженные в ХХ веке, в фундамент нашей системы единиц измерения. Тут же целая куча единиц преобразования и фундаментальных констант станут известны с большей точностью (убедитесь, что у вас новый бланк CODATA, и держите карточку с новыми значениями констант при себе до тех пор, пока вы не запомните их наизусть). Это откроет путь к новой физике и новым технологиям. В случае, если вы решите проводить ваши собственные эксперименты, определяющие значения констант, имейте в виду, что крайний срок для включения полученных вами значений — 1 июля 2017 года.
Переход от платино-иридиевого килограмма, исторически обозначаемого символом
 , к килограмму на основе постоянной Планка h может хорошо визуализироваться графически как 3D-объект, который
содержит оба символа. При вращении виден плавный переход от формы
проекции из
, к килограмму на основе постоянной Планка h может хорошо визуализироваться графически как 3D-объект, который
содержит оба символа. При вращении виден плавный переход от формы
проекции из  в h, олицетворяющий собой более 200 лет прогресса в области метрологии и физики:
в h, олицетворяющий собой более 200 лет прогресса в области метрологии и физики:
Заинтересованный читатель может заказать красивую 3D-версию здесь. Это идеальный подарок для вашего значимого человека на Рождество (чтобы быть готовым к переопределению 2018 года), и вы можете заказать его в виде подвески или серег (доступно исполнение в различных металлах; платина, очевидно, самый естественный выбор, однако такой символ будет стоить около 5000 долларов, так что вариант с полированным серебром тоже неплох).
Вот некоторые образы золотых версий
 Toh3D:
Toh3D:
Я понимаю, что не все так, как я, взволнованы этими событиями. Я жду 2018 года, когда килограмм как материальный артефакт уйдет в отставку и его заменит фундаментальная константа. Новая СИ будет основывать самые важные стандарты измерения на технологиях XXI века.
Если у вас возникли вопросы или есть комментарии — не стесняйтесь: пишите мне на jeancharlesdeborda@gmail.com; благодаря последним достижениям в области технологических последствий (EPR = ER) у нас появилась более быстрая связь с Землей.
À tous les temps, à tous les peuples!
Вернуться назад