Математики о системных дефектах ЕГЭ (Малинецкий Г.Г.)
29-09-2009, 12:14. Разместил: Yary
Он был призван стать и итоговой аттестацией для выпускников, и вступительным испытанием для абитуриентов, и инструментом мониторинга системы образования, и средством контроля объективно-сти школьных оценок. Однако при решении любой конкретной задачи универсальный инструмент неизбежно проигрывает специализированным (так, гусь летает, но значительно хуже орла, поет, но значительно хуже соловья, плавает, но значительно хуже пингвина, и бегает, но значительно хуже страуса). В частности, итоговая аттестация и вступительное испытание оказываются несовместимы по целому ряду причин, перечисленных в таблице.
| Итоговая аттестация | Вступительное испытание | |
| Тип испытания | Тест достижений (взгляд в прошлое) | Тест способностей (взгляд в будущее) |
| Цель испытания | Выявление худших | Выявление лучших |
| Участие в экза-мене | Обязательное | Добровольное |
| Оценка подго-товленности | Абсолютная (сравнение с некоторым стандартом) | Относительная (сравнение с другими экзаменуемыми) |
| Тип теста (по решаемой задаче) | Критериально-ориентированный (проверка усвоения учебного мате-риала) | Нормативно-ориентированный (ранжи-ровка испытуемых) |
| Содержательный смысл балла | Доля усвоенных знаний, умений и навыков из обяза-тельного набора | Доля конкурентов, хуже ос-воивших предмет |
| Необходимая шкала оценок | Нормированная (определено начало отсчета) | Метрическая (определена цена каждого балла, но не начало отсчета) |
Данная несовместимость вылилась в целый ряд вторичных дефектов. Остановимся на них подробнее.
ИТОГОВАЯ АТТЕСТАЦИЯ
Функция единого государственного экзамена как итоговой аттестации по-степенно сходит на нет. Еще недавно как одно из важнейших достоинств ЕГЭ превозносилась его дифференцирующая способность, значительно более высокая, чем у оценок среднестатистического учителя. Сейчас же выпускной экзамен свелся к недифференцированному зачету, который обязателен всего по двум предметам – по русскому языку и математике. Попробуем понять, что же означает подтверждение освоения «основных общеобразовательных программ среднего (полного) общего образования в 2009 году» по этим предметам, без которого нельзя получить аттестат. Контрольно-измерительные материалы ЕГЭ по математике содержат 10 заданий части A с выбором ответа из четырех предложенных вариантов. При этом необходимо дать всего 4 верных ответа, чтобы избежать двойки. Если не знать совсем ничего и расставлять крестики наугад, то пройти итоговую атте-стацию удается примерно в 2 случаях из 9. Однако, опираясь даже на фрагментарные знания или хотя бы на здравый смысл, вероятность успеха можно существенно повысить. Определим владение предметом как долю тех простых заданий, с которыми испытуемый может справиться, и будем считать, что в остальных случаях он просто гадает. В реальности не всегда имеет место четкое разделение на «знаю» или «гадаю», а часто происходит отбрасывание некоторых неверных вариантов ответа и случайный выбор между оставшимися вариантами. Однако математически эти ситуации однозначно связаны. Так, если испытуемый справляется с заданием с вероятностью p, а с вероятностью 1 p случайно выбирает один вариант ответа из n предложенных, то в среднем это эквивалентно уменьшению числа возможных вариантов до
n' = n / ((n 1)∙p + 1).
Зависимость вероятности подтвердить освоение общеобразовательной программы по математике от владения предметом приведена на рис. 1.
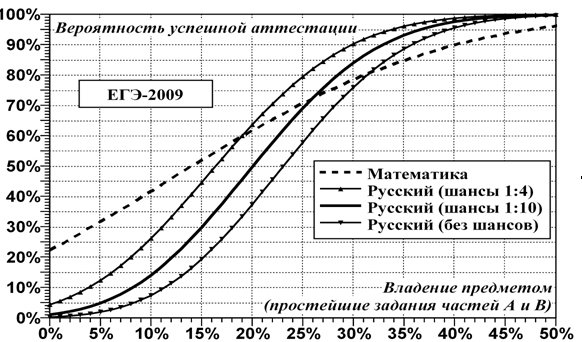
Рис. 1.
Видно, что крайне слабые знания обеспечивают довольно высокую вероятность успешной аттестации, которая достигает 50% при владении предметом на уровне всего 14%.
Ситуация с ЕГЭ по русскому языку несколько менее однозначная. Здесь почти нереально получить зачет, только расставляя наугад крестики, поскольку необходимо набрать 15 баллов, а (однобалльных) заданий в части A всего лишь 30. Однако в контрольно-измерительных материалах по русскому языку ответ на задания части B, в которой разыгрывается еще 9 баллов, тоже выбирается из приведенного набора вариантов (в отличие от математики, где ответы в части B нужно получать самостоятельно). Эти варианты заведомо неравноценны, а их число непостоянно, в силу чего нельзя достоверно определить шансы на успех при угадывании ответов для заданий части B, но могут быть сформулированы следующие три гипотезы:
оптимистичная – шансы угадать такие же, как и для части A, т.е. 1 : 4;
реалистичная – шансы угадать примерно 1 : 10;
пессимистичная – шансов угадать нет вообще.
Как видно из рисунка, переход от оптимистичной гипотезы к пессимистичной эквивалентен изменению владения предметом примерно на 5%, т.е. особой разницы между крайними гипотезами нет, и разумно опираться на промежуточную реалистичную. Зависимости для математики и русского языка качественно довольно похожи, но количественно всё же различны, поэтому в простейшем случае уместно ориентироваться на точку пересечения графиков. Из ее положения можно сделать общий вывод, что 70% вероятность подтверждения освоения основных общеобразовательных программ по этим предметам обеспечивается владени-ем ими на уровне только в 25%. А уровень владения в 33,3% (соответствующий пресловутому «попросим компьютер убрать два неверных ответа из четырех») поднимает вероятность успеха и вовсе до 80÷90%. Очевидно, что ценность подобной аттестации (заметим, даже не затрагивающей самых сложных заданий части C) близка к нулю...
Г.Г. Малинецкий,доктор физико-математических наук, Институт прикладной математики им. М.В. Келдыша РАН
Полный текст статьи Г.Г. Малинецкого и А.В. Подлазова будет напечатан в октябрьском журнале "Научный эксперт".
Вернуться назад