Пифагор был гений-математик? Но не по шумерским стандартам.

Выясняется, что за более чем 1000 лет до вычисленной Пифагором длины гипотенузы, в Месопотамии работали с теми же теоремами, чтобы вычислять площадь сельскохозяйственных угодий. Обнаружены массы глиняных табличек, на которых шумерские студенты решали свои математические задачи, клиновидно впечатывая в глину заостренный конец тростника.

Найденные таблички несут доказательства существования практической, а также более сложной теоретической математики и показывают, насколько легко шумеры обращались со сложными вычислениями - более тысячелетия до Р.Х., т.е. делали то, что не все европейцы могли делать после Пифагора и Евклида и что по сей день не могут делать некоторые недоучившиеся эффективные менеджеры, что в прочем не мешает им быть успешными в потреблении.

"Это было почти 4.000 лет тому назад, и не существовало других древних культур того времени, которые нам известны, что делали подобное уровню той работы. Это, кажется, выходит за рамки всех потребностей повседневной жизни", сказал Александр Джонс, профессор истории точных наук Нью-Йоркского университета.

Разумеется, говоря что таблички были "обнаружены" - не значит, что они были откопаны вот только что американцами, принесшими в Ирак демократию и просвещение. Они были обнаружены при раскопках Ниппура в период с середины 19-го века до 1920-х годов. И они, частью благополучно, сохранились до наших времен в ящиках наполненных соломой. Но вот интерес к ним проявили только сейчас.

Возможно это т.н. "вавилоны", для пропорционирова ния длин (если посмотрите, то на них имеются отметины).

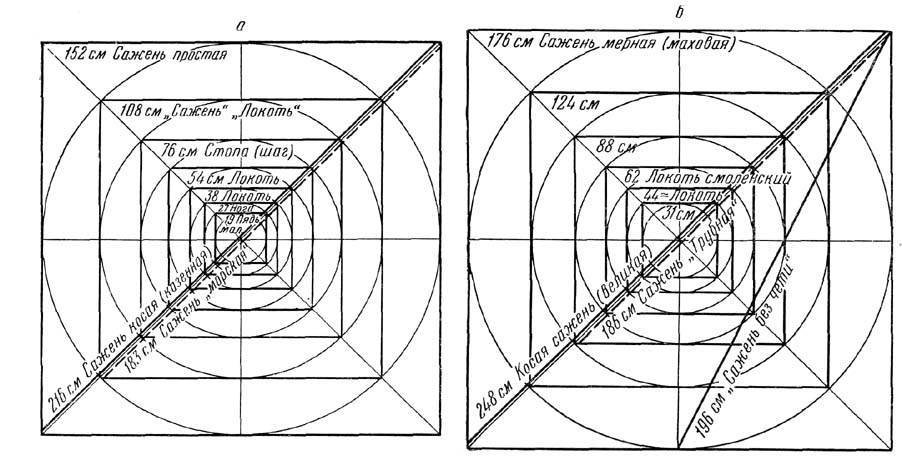
Поскольку метод "вавилонов", как свидетельствуют находки, применялся древними мастерами для пропорционирова ния саженей по некоторым эталонам, то естественно, что они пользовались им без знания дробей и извлечения корня. Не исключено, однако, что они использовали способы восстановления размеров по любой сохранившейся сажени и даже при отсутствии эталона - по любому прутку с размером, близким к пропорции, человека, например построением треугольных фигур. Этот метод можно назвать методом "наугольников" (наугольник - плотницкий инструмент треугольной формы [5]). Он заключается в следующем (рис 4):

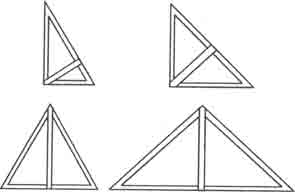
допустим, что эталонная сажень не сохранилась и ее требуется восстановить. Тогда берется деревянный пруток длиной, допустим, в рост плотника. Возьмем для примера рост плотника 172 см, что почти соответствует мерной (маховой) сажени, и примем его за базисную длину. Если три прутка данной длины сложить равнобедренным наугольником, то высота в нем будет равна 148,96 см, что по структуре соответствует сажени простой, да и по длине близко к ней. Если к центру мерной сажени под прямым углом приставить другую мерную сажень и соединить их свободные концы длинными прутками, то получим равносторонний наугольник, длинные стороны которого равны 192,30 см, а это аналог "сажени без чети". Возьмем две полученные простые сажени, соединим их концы под прямым углом и, соединив свободные концы длинным прутком, получим расстояние, равное 210,66 см - аналог сажени косой. Если такую же операцию проведем мерными саженями, получим длину 243,24 см - по назначению аналог сажени великой. И последняя сажень - трубная. Последняя получается, когда к центру косой сажени под прямым углом приставляется сажень простая. При соединении их свободных концов получают равносторонний наугольник, две стороны которого будут иметь длину 182,44 см, что как раз и является аналогом длины трубной сажени.